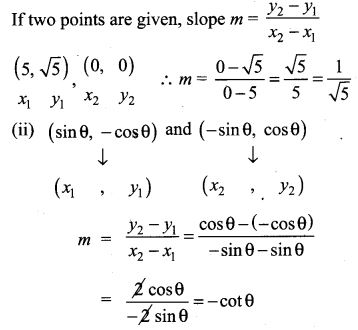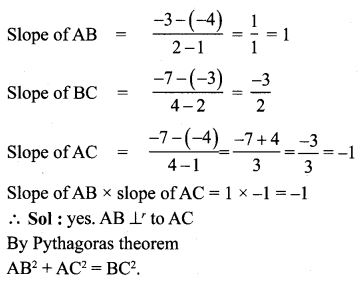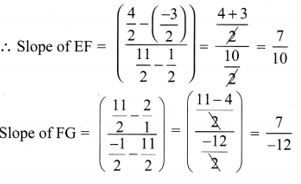10th Maths Book Back Question and Answers – Chapter 5 Exercise 5.2:

Samacheer Kalvi 10th Standard Maths Book Back Questions with Answers PDF uploaded and the same given below. Class-tenth candidates and those preparing for TNPSC exams can check the Maths Book Back Answers PDF below. Samacheer Kalvi Class 10th Std Maths Book Back Answers Chapter 5 Coordinate Geometry Exercise 5.2 Solutions are available below. Check the complete Samacheer Kalvi 10th Maths – Coordinate Geometry Ex 5.2 Book Back Answers below:

We also provide class 10th other units Maths Book Back One, Two, and Five Mark Solutions Guide on our site. Students looking for the 10th standard Maths Ex 5.2 – Coordinate Geometry Book Back Questions with Answer PDF

For the complete Samacheer Kalvi 10th Maths Book Back Solutions Guide PDF, check the link – Samacheer Kalvi 10th Maths Book Back Answers

Samacheer Kalvi 10th Maths Book Back Answers – Ex 5.2 Coordinate Geometry

Samacheer Kalvi 10th Maths Book Subject One Mark, Two Mark, Five Mark Guide questions and answers are below. Check Maths Book Back Questions with Answers. Take the printout and use it for exam purposes.

For Samacheer Kalvi 10th Maths Book PDF, check the link – 10th Maths Book PDF

Chapter 5

Exercise 5.2 Coordinate Geometry

1. What is the slope of a line whose inclination with the positive direction of x -axis is
(i) 90°
(ii) 0°
Solution:
(i) θ = 90°
m = tan θ = tan 90° = ∝ (undefined)
(ii) m = tan θ = tan 0° = 0

2. What is the inclination of a line whose slope is (i) = 0
Solution:
(i) Slope = 0
tan θ = 0
tan 0 = 0
∴ θ = 0°

(ii) Slope = 1
tan θ = 1
tan 45° = 1
∴ θ = 45°
angle of inclination is 45°

3. Find the slope of a line joining the points
(i) (5, 5–√)) with origin
(ii) (sin θ, -cos θ) and (-sin θ, cos θ)
(i) (5, 5–√)) with origin (0, 0)
Solution:

4. What is the slope of a line perpendicular to the line joining A(5, 1) and P where P is the mid-point of the segment joining (4, 2) and (-6,4).
Solution:
P is the midpoint of the segment joining (4, 2) and (-6, 4)

5. Show that the given points are collinear (-3, -4), (7, 2), and (12, 5)
Solution:
The vertices are A(-3, -4), B(7, 2), and C (12, 5)

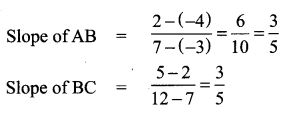
The slope of AB = Slope of BC
∴ The points A, B, and C lie on the same line.
∴ They are collinear.

6. If the three points (3, -1), (a, 3), (1, -3) are collinear, find the value of a.
Solution:
The slope of AB = slope of BC.

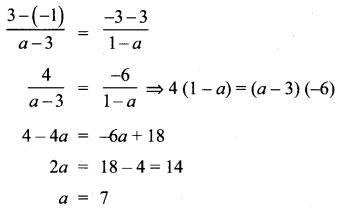
7. The line through the points (-2, a) and (9, 3) has a slope –12. Find the value of a.
Solution:
A line joining the points (-2, a) and (9, 3) has a slope m = –12.

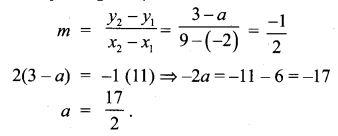
8. The line through the points (-2, 6) and (4, 8) is perpendicular to the line through the points (8, 12) and (x, 24) . Find the value of x.
Solution:

9. Show that the given points form a right-angled triangle and check whether they satisfy pythagoras theorem
(i) A(1, -4), B(2, -3) and C(4, -7)
(ii) L(0, 5), M(9, 12) and N(3, 14)
Solution:

10. Show that the given points form a parallelogram : A(2.5, 3.5), B(10, -4), C(2.5, -2.5) and D(-5, 5)
Solution:

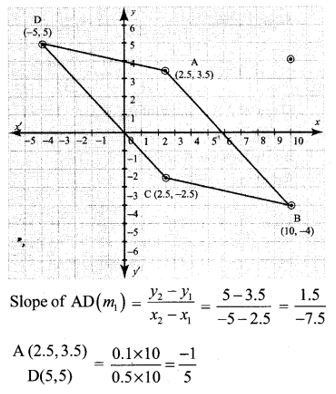
∴ The given points form a parallelogram.

11. If the points A(2, 2), B(-2, -3), C(1, -3) and D(x, y) form a parallelogram then find the value of x and y.
Solution:
A(2, 2), B(-2, -3), C(1, -3), D(x, y)

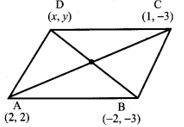
Since ABCD forms a parallelogram, slope of opposite sides are equal and diagonals bisect each other.
Mid point of BD = Mid point of AC

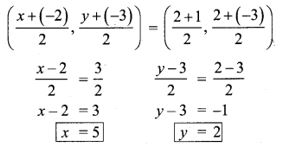
12. Let A(3, -4), B(9, -4), C(5, -7) and D(7, -7). Show that ABCD is a trapezium.
Solution:
A (3, -4), B (9, -4), C (5, -7) and D (7, -7)

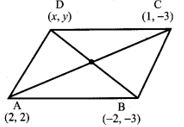
If only one pair of opposite sides of a quadrilateral are parallel, then it is said to be a trapezium.

∴ One pair of opposite sides are parallel.
∴ ABCD is a trapezium.

13. A quadrilateral has vertices at A(- 4, -2), B(5, -1) , C(6, 5) and D(-7, 6). Show that the mid-points of its sides form a parallelogram
Solution:

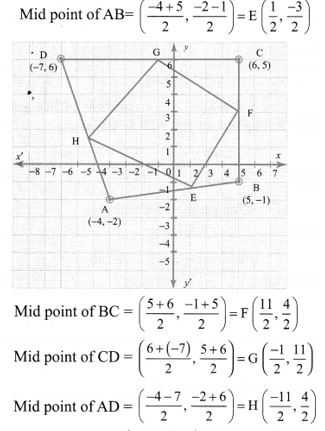
In a parallelogram, diagonals bisect each other. Opposite sides are parallel as their slopes are equal the midpoints of the diagonals are the same.
∴ Midpoints of the sides of a quadrilateral form a parallelogram.

Other Important Links for 10th Maths Book Back Answers Solutions:

For 10th Maths Chapter 5 book back question and answers, check the link – Samacheer kalvi 10th Maths Chapter 5 Coordinate Geometry

Click here for the complete Samacheer Kalvi 10th Maths Book Back Solution Guide PDF – 10th Maths Book Back Answers