Samacheer kalvi 10th Maths - Trigonometry Ex 6.4

10th Maths Book Back Question and Answers – Chapter 6 Exercise 6.4:

Samacheer Kalvi 10th Standard Maths Book Back Questions with Answers PDF uploaded and the same given below. Class-tenth candidates and those preparing for TNPSC exams can check the Maths Book Back Answers PDF below. Samacheer Kalvi Class 10th Std Maths Book Back Answers Chapter 6 Trigonometry Exercise 6.4 Solutions are available below. Check the complete Samacheer Kalvi 10th Maths – Trigonometry Ex 6.4 Book Back Answers below:

We also provide class 10th other units Maths Book Back One, Two, and Five Mark Solutions Guide on our site. Students looking for the 10th standard Maths Ex 6.4 – Trigonometry Book Back Questions with Answer PDF

For the complete Samacheer Kalvi 10th Maths Book Back Solutions Guide PDF, check the link – Samacheer Kalvi 10th Maths Book Back Answers

Samacheer Kalvi 10th Maths Book Back Answers – Ex 6.4 Trigonometry

Samacheer Kalvi 10th Maths Book Subject One Mark, Two Mark, Five Mark Guide questions and answers are below. Check Maths Book Back Questions with Answers. Take the printout and use it for exam purposes.

For Samacheer Kalvi 10th Maths Book PDF, check the link – 10th Maths Book PDF

Chapter 6 Exercise 6.4 Trigonometry

1. From the top of a tree of a height of 13 m the angle of elevation and depression of the top and bottom of another tree is 45° and 30° respectively. Find the height of the second tree. (3–√ = 1.732)
Solution:

2. A man is standing on the deck of a ship, which is 40 m above water level. He observes the angle of elevation of the top of a hill as 60° and the angle of depression of the base of the hill as 30°. Calculate the distance of the hill from the ship and the height of the hill. (3–√ = 1.732)
Solution:

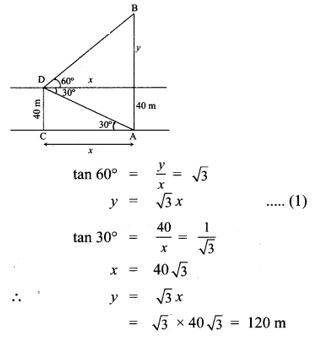
∴ The height of the hill = 120 + 40 = 160 m
The distance of the hill from the ship is AC = x = 403–√ m = 69.28 m

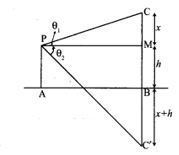
3. If the angle of elevation of a cloud from a point ‘h’ meters above a lake is θ₁ and the angle of depression of its reflection in the lake is θ₂. Prove that the height that the cloud is located from the ground is h(tanθ1+tanθ2)tanθ2−tanθ1
Solution:

Let AB be the surface of the lake and let p be the point of observation such that AP = h meters.
Let C be the position of the cloud and C’ be its reflection in the lake. Then CB = C’B.
Let PM be ⊥^r from P on CB
Then ∠CPM = θ₁, and ∠MPC = θ₂
Let CM = x.
Then CB = CM + MB = CM + PA
= x + h

Hence proved.

4. The angle of elevation of the top of a cell phone tower from the foot of a high apartment is 60° and the angle of depression of the foot of the tower from the top of the apartment is 30°. If the height of the apartment is 50 m, find the height of the cell phone tower. According to radiations control norms, the minimum height of a cell phone tower should be 120 m. State if the height of the above-mentioned cell phone tower meets the radiation norms.
Solution:

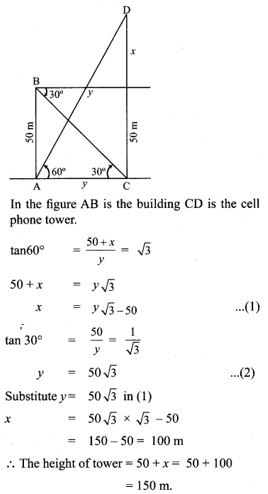
Since 150m > 120m, yes the height of the above-mentioned tower meets the radiation norms.

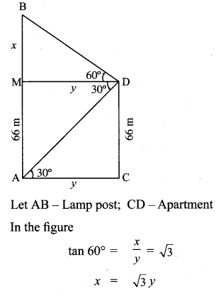
5. The angles of elevation and depression of the top and bottom of a lamp post from the top of a 66 m high apartment are 600 and 30° respectively. Find
(i) The height of the lamp post.
(ii) The difference between the height of the lamp post and the apartment.
(iii) The distance between the lamp post and the apartment. (3–√ = 1.732)
Solution:

= 114.312 m.

6. Three villagers A, B, and C can see each T other across a valley. The horizontal distance between A and B is 8 km and the horizontal distance between B and C is 12 km. The angle of depression of B from A is 20° and the angle of elevation of C from B is 30°. Calculate :

(i) the vertical height between A and B.
(ii) the vertical height between B and C. (tan20° = 0.3640, 3–√ = 1.732)

Solution:

How To Get Govt. Job Without Wasting Years?
CLICK HERE

06 Apr 2022