10th Maths Book Back Question and Answers – Chapter 4 Exercise 4.5:
Samacheer Kalvi 10th Standard Maths Book Back Questions with Answers PDF uploaded and the same given below. Class-tenth candidates and those preparing for TNPSC exams can check the Maths Book Back Answers PDF below. Samacheer Kalvi Class 10th Std Maths Book Back Answers Chapter 4 Geometry Exercise 4.5 Solutions are available below. Check the complete Samacheer Kalvi 10th Maths – Geometry Ex 4.5 Book Back Answers below:
We also provide class 10th other units Maths Book Back One, Two, and Five Mark Solutions Guide on our site. Students looking for the 10th standard Maths Ex 4.5- Geometry Book Back Questions with Answer PDF
For the complete Samacheer Kalvi 10th Maths Book Back Solutions Guide PDF, check the link – Samacheer Kalvi 10th Maths Book Back Answers
Samacheer Kalvi 10th Maths Book Back Answers – Ex 4.5 Geometry
Samacheer Kalvi 10th Maths Book Subject One Mark, Two Mark, Five Mark Guide questions and answers are below. Check Maths Book Back Questions with Answers. Take the printout and use it for exam purposes.
For Samacheer Kalvi 10th Maths Book PDF, check the link – 10th Maths Book PDF
Chapter 4
Exercise 4.5 Geometry
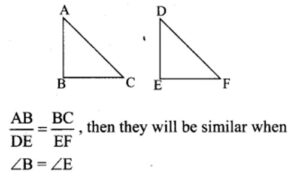
1. If in triangles ABC and EDF, ABDE=BCFD then they will be similar, when
(1) ∠B = ∠E
(2) ∠A = ∠D
(3) ∠B = ∠D
(4) ∠A = ∠F
Solution:
(1) ∠B = ∠E
Hint:
2.In, ∆LMN, ∠L = 60°, ∠M =50° . If ∆LMN ~ ∆PQR then the value of ∠R is
(1) 40°
(2) 70°
(3) 30°
(4) 110°
Solution:
(2) 70°
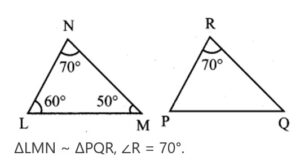
∆LMN ~ ∆PQR, ∠R = 70°.
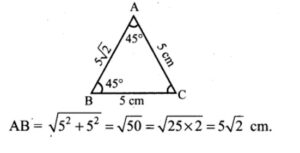
3.If ∆ABC is an isosceles triangle with ∠C = 90° and AC = 5 cm, then AB is
(1) 2.5 cm
(2) 5 cm
(3) 10 cm
(4) 52–√ cm
Solution:
(4) 52–√cm
Hint:
4.In a given figure ST || QR, PS = 2 cm and SQ = 3 cm. Then the ratio of the area of ∆PQR to the area of ∆PST is
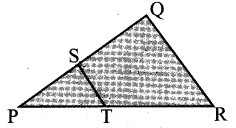
(1) 25 : 4
(2) 25 : 7
(3) 25 : 11
(4) 25 : 13
Solution:
(1) 25 : 4
Hint:
Ratio of the area of similar triangles is equal to the ratio of the square of their corresponding sides.
∴ 52 : 22 = 25 : 4
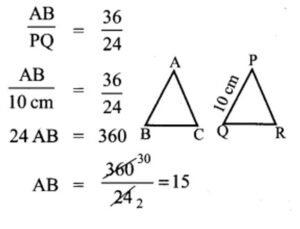
5.The perimeters of two similar triangles ∆ABC and ∆PQR are 36 cm and 24 cm respectively. If PQ = 10 cm, then the length of AB is

Solution:
(4) 15 cm
Hint:
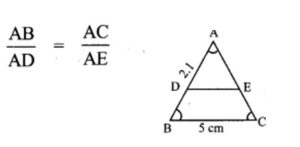
6.If in ∆ABC, DE || BC . AB = 3.6 cm, AC = 2.4 cm and AD = 2.1 cm then the length of AE is
(1) 1.4 cm
(2) 1.8 cm
(3) 1.2 cm
(4) 1.05 cm
Solution:
(1) 1.4 cm
3⋅62⋅1=2⋅4A⋅E
(3.6) (AE) = 2.1 × 2.4
AE = 1.4 cm
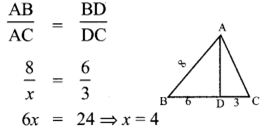
7.In a ∆ABC , AD is the bisector of ∠BAC . If AB = 8 cm, BD = 6 cm and DC = 3 cm. The length of the side AC is
(1) 6 cm
(2) 4 cm
(3) 3 cm
(4) 8 cm
Solution:
(2) 4 cm
Hint:
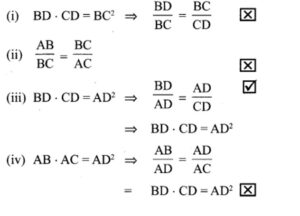
8. In the adjacent figure ∠BAC = 90° and AD ⊥ BC then
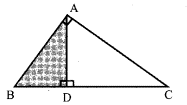
(1) BD.CD = BC2
(2) AB.AC = BC2
(3) BD.CD = AD2
(4) AB.AC = AD2
Solution:
(3) BD.CD = AD2
9. Two poles of heights 6 m and 11 m stand vertically on a plane ground. If the distance between their feet is 12 m, what is the distance between their tops?
(1) 13 cm
(2) 14 m
(3.) 15 m
(4) 12.8 m
Solution:
(1) 13 cm
Hint:
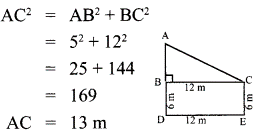
10.In the given figure, PR = 26 cm, QR = 24 cm, PAQ = 90° , PA = 6 cm and QA = 8 cm. Find ∠PQR
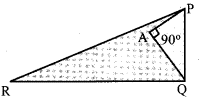
(1) 80°
(2) 85°
(3) 75°
(4) 90°
Solution:
(4) 90°
Hint:
PR = 26
QR = 24
∠PAQ = 90°
PQ = 10
PQ = 262−242−−−−−−−−√=100−−−√ = 10
∴ ∠PAQ = 90°
11.A tangent is perpendicular to the radius at the …………..
(1) centre
(2) point of contact
(3) infinity
(4) chord
Answer:
(2) point of contact
12.How many tangents can be drawn to the circle from an exterior point?
(1) one
(2) two
(3) infinite
(4) zero
Solution:
(2) two
13. The two tangents from an external points P to a circle with centre at O are PA and PB. If ∠APB = 70° then the value of ∠AOB is
(1) 100°
(2) 110°
(3) 120°
(4) 130°
Solution:
(2) 110°
Hint:
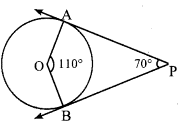
14.In figure CP and CQ are tangents to a circle T with centre at O. ARB is another tangent touching the circle at R. If CP = 11 cm and BC = 7 cm, then the length of BR is
(1) 6 cm
(2) 5 cm
(3) 8 cm
(4) 4 cm
Solution:
(4) 4 cm
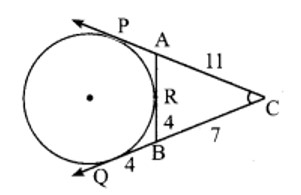
BQ = BR
CP = CQ = 11
BC = 7, ∴ BQ = CQ – BC
= 11 – 7 = 4
BR = BQ = 4cm
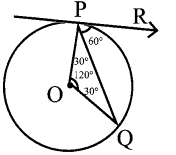
15.In figure if PR is tangent to the circle at P and O is the centre of the circle, then ∠POQ is
(1) 120°
(2) 100°
(3) 110°
(4) 90°
Solution:
(1) 120°
∠POQ = 180° -(30° + 30°)
= 180° – 60°
= 120°
1 .In the figure, if BD⊥AC and CE ∠ AB, prove that
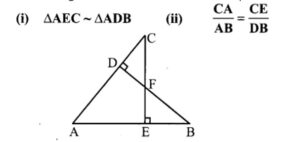
Solution:
In the figure’s ∆AEC and ∆ADB.
We have ∠AEC =∠ADB = 90 (∵ CE ∠AB and BD ∠AC)
and ∠EAC =∠DAB
[Each equal to ∠A]
Therefore by AA-criterion of similarity, we have ∆AEC ~ ∆ADB
(ii) We have
∆AEC ~ ∆ADB [As proved above]
⇒ CABA=ECDB⇒CAAB=CEDB
Hence proved.
2. In the given figure AB||CD || EF. If AB = 6 cm, CD = x cm, EF = 4 cm, BD = 5 cm and DE = y cm. Find x and y.
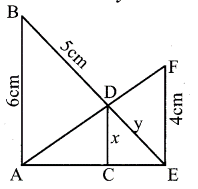
Solution:
In the given figure, ∆AEF, and ∆ACD are similar ∆s.
∠AEF = ∠ACD = 90°
∠A = ∠A (common)∴ ∆AEF ~ ∆ACD (By AA criterion of similarity)


Substituting x = 2.4 cm in (3)
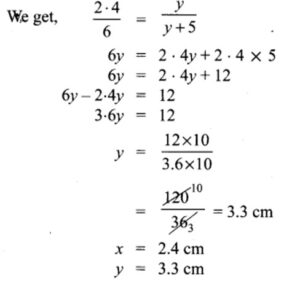
3. O is any point inside a triangle ABC. The bisector of ∠AOB , ∠BOC and ∠COA meet the sides AB, BC and CA in point D, E and F respectively.
Show that AD × BE × CF = DB × EC × FA
Solution:
In ∆AOB, OD is the bisector of ∠AOB.
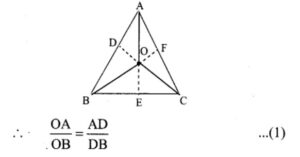
In ∆BOC, OE is the bisector of ∠BOC
∴ OBOC=BEEC …………. (2)
In ∆COA, OF is the bisector of ∠COA.
∴ OCOA=CFFA …………… (3)
Multiplying the corresponding sides of (1), (2) and (3), we get

⇒ DB × EC × FA = AD × BE × CF
Hence proved.
4. In the figure, ABC is a triangle in which AB = AC. Points D and E are points on the side AB and AC respectively such that AD = AE . Show that the points B, C, E, and D lie on the same circle.
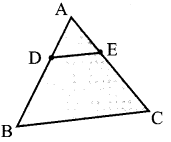
Solution:
In order to prove that the points B, C, E, and D are concyclic, it is sufficient to show that ∠ABC + ∠CED = 180° and ∠ACB + ∠BDE = 180°.
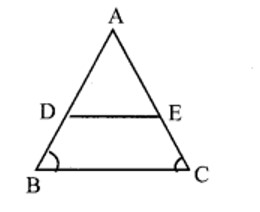
In ∆ABC, we have AB = AC and AD = AE.
⇒ AB – AD = AC – AE
⇒ DB = EC
Thus we have AD = AE and DB = EC. (By the converse of Thale’s theorem)
⇒ ADDB=AEEC ⇒ DE||BC
∠ABC = ∠ADE (corresponding angles)
⇒ ∠ABC + ∠BDE = ∠ADE + ∠BDE (Adding ∠BDE on both sides)
⇒ ∠ABC + ∠BDE = 180°
⇒ ∠ACB + ∠BDE = 180° (∵ AB = AC ∴ ∠ABC = ∠ACB)
Again DE || BC
⇒ ∠ACB = ∠AED
⇒ ∠ACB + ∠CED = ∠AED + ∠CED (Adding ∠CED on both sides).
⇒ ∠ACB + ∠CED = 180° and
⇒ ∠ABC + ∠CED = 180° (∵ ∠ABC = ∠ACB)
Thus BDEC is a quadrilateral such that
⇒ ∠ACB + ∠BDE = 180° and
⇒ ∠ABC + ∠CED = 180°
∴ BDEC is a cyclic quadrilateral. Hence B, C, E, and D are concyclic points.
5. Two trains leave a railway station at the same time. The first train travels due west and the second train is due north. The first train travels at a speed of 20 km/hr and the second train travels at 30 km/hr. After 2 hours, what is the distance between them?
Solution:
After 2 hours, let us assume that the first train is at A and the second is at B.

6.D is the mid point of side BC and AE⊥BC. If i BC a, AC = b, AB = c, ED = x, AD = p and AE = h , prove that
(i) b2 = p2 + ax + a24
(ii) c2 = p2 – ax + a24
(iii) b2 + c2 = 2p2 + a22
Solution:
From the figure, D is the mid point of BC.
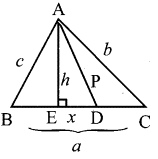
We have ∠AED = 90°
∴ ∠ADE < 90° and ∠ADC > 90°
i.e. ∠ADE is acute and ∠ADC is obtuse,
(i) In ∆ADC, ∠ADC is an obtuse angle.
AC2 = AD2 + DC2 + 2DC × DE
⇒ AC2 = AD2 + 12 BC2 + 2 . 12 BC . DE
⇒ AC2 = AD2 + 14 BC2 + BC . DE
⇒ AC2 = AD2 + BC . DE + 14 BC2
⇒ b2 = p2 + ax + 14 a2
Hence proved.
(ii) In ∆ABD, ∠ADE is an acute angle.
AB2 = AD2 + BD2 – 2BD . DE
⇒ AB2 = AD2 + (12BC)2 – 2 × 12 BC . DE
⇒ AB2 = AD2 + 14 BC2 – BC . DE
⇒ AB2 = AD2 – BC . DE + 14 BC2
⇒ c2 = p2 – ax + 14 a2
Hence proved.
(iii) From (i) and (ii) we get .
AB2 + AC2 = 2AD2 + 12 BC2
i.e. c2 + b2 = 2p2 + a22
Hence it is proved.
7. A man whose eye level is 2 m above the ground wishes to find the height of a tree. He places a mirror horizontally on the ground 20 m from the tree and finds that if he stands at a point C which is 4 m from mirror B, he can see the reflection of the top of the tree. How height is the tree?
Solution:
From the figure; ∆DAC, ∆FBC are similar triangles and ∆ACE & ∆ABF are similar triangles.
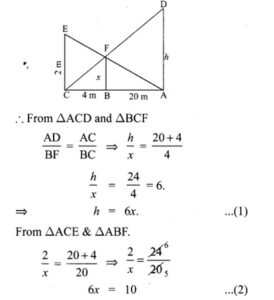
∴ height of the tree h = 6x = 10 m.
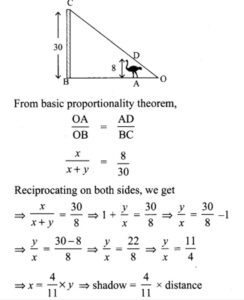
8. An emu which is 8 ft tall standing at the foot of a pillar which is 30 ft height. It walks away from the pillar. The shadow of the emu falls beyond emu. What is the relation between the length of the shadow and the distance from the emu to the pillar?
Solution:
Let OA (emu shadow) the x and AB = y.
⇒ pillar’s shadow = OB = OA + AB
⇒ OB = x + y
9. Two circles intersect at A and B. From a point, P on one of the circle’s lines PAC and PBD are drawn intersecting the second circle at C and D. Prove that CD is parallel to the tangent at P.
Solution:
Let XY be the tangent at P.
TPT: CD is || to XY.
Construction: Join AB.
ABCD is a cyclic quadilateral.
∠BAC + ∠BDC= 180° ………… (1)
∠BDC = 180° – ∠BAC …………. (2)
Equating (1) and (2)
we get ∠BDC = ∠PAB
Similarly we get ∠PBA = ∠ACD
as XY is tangent to the circle at ‘P’
∠BPY = ∠PAB (by alternate segment there)
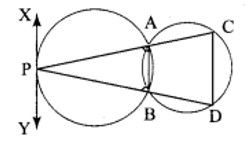
∴ ∠PAB = ∠PDC
∠BPY = ∠PDC
XY is parallel of CD.
Hence proved.
10. Let ABC be a triangle and D, E, F are points on the respective sides AB, BC, AC (or their extensions). Let AD: DB = 5 : 3, BE : EC = 3 : 2 and AC = 21. Find the length of the line segment CF.
Solution:
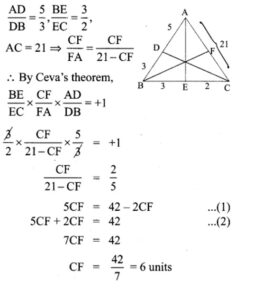
Other Important Links for 10th Maths Book Back Answers Solutions:
For 10th Maths Chapter 4 book back question and answers, check the link – Samacheer kalvi 10th Maths Chapter 4 Geometry
Click here for the complete Samacheer Kalvi 10th Maths Book Back Solution Guide PDF – 10th Maths Book Back Answers

it is very easy to lean one mark