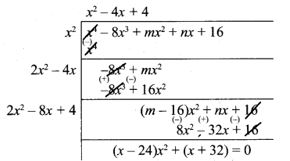10th Maths Book Back Question and Answers – Chapter 3 Exercise 3.8:

Samacheer Kalvi 10th Standard Maths Book Back Questions with Answers PDF uploaded and the same given below. Class-tenth candidates and those preparing for TNPSC exams can check the Maths Book Back Answers PDF below. Samacheer Kalvi Class 10th Std Maths Book Back Answers Chapter 3 Exercise 3.8 Solutions are available below. Check the complete Samacheer Kalvi 10th Maths – Algebra Ex 3.8 Book Back Answers below:

We also provide class 10th other units Maths Book Back One, Two, and Five Mark Solutions Guide on our site. Students looking for the 10th standard Maths Ex 3.8 – Algebra Book Back Questions with Answer PDF

For the complete Samacheer Kalvi 10th Maths Book Back Solutions Guide PDF, check the link – Samacheer Kalvi 10th Maths Book Back Answers

Samacheer Kalvi 10th Maths Book Back Answers – Ex 3.8 Algebra

Samacheer Kalvi 10th Maths Book Subject One Mark, Two Mark, Five Mark Guide questions and answers are below. Check Maths Book Back Questions with Answers. Take the printout and use it for exam purposes.

For Samacheer Kalvi 10th Maths Book PDF, check the link – 10th Maths Book PDF

Chapter 3

Exercise 3.8 Algebra

1. Find the square root of the following polynomials by division method
(i) x⁴ – 12x³ + 42x² – 36x + 9
(ii) 37x² – 28x³ + 4x⁴ + 42x + 9
(iii) 16x⁴ + 8x² + 1
(iv) 121x⁴ – 198x³ – 183x² + 216x + 144
Solution:
The long division method in finding the square root of a polynomial is useful when the degrees of a polynomial is higher.

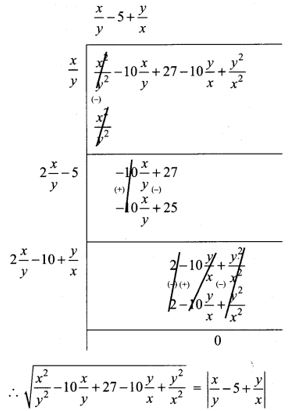
2. Find the square root of the expression x2y2−10xy+27−10yx+y2x2
Solution:

3. Find the values of a and b if the following polynomials are perfect squares
(i) 4x⁴ – 12x³ + 37x² + bx + a
(ii) ax⁴ + bx³ + 361ax² + 220x + 100
Solution:
(i)

Since it is a perfect square.
Remainder = 0
⇒ b + 42 = 0, a – 49 = 0
b = -42, a = 49

(ii) ax⁴ + bx³ + 361ax² + 220x + 100

Since remainder is 0
a = 144
b = 264

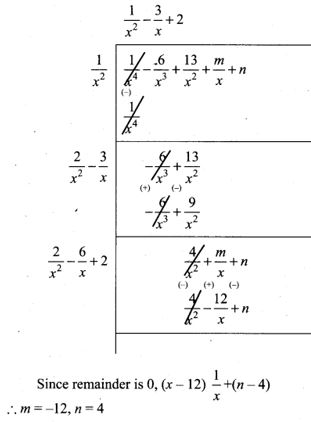
4. Find the values of m and n if the following expressions are perfect squares
(i) 1×4−6×3+13×2+mx+n
(ii) x⁴ – 8x³ + mx² + nx + 16
Solution:
(i)

(ii)

Since the remainder is 0,
m = 24, n = -32

Other Important Links for 10th Maths Book Back Answers Solutions:

For 10th Maths Chapter 3 book back question and answers, check the link – Samacheer kalvi 10th Maths Chapter 3 Algebra

Click here for the complete Samacheer Kalvi 10th Maths Book Back Solution Guide PDF – 10th Maths Book Back Answers