10th Maths Book Back Question and Answers – Chapter 3 Exercise 3.15:

Samacheer Kalvi 10th Standard Maths Book Back Questions with Answers PDF uploaded and the same given below. Class-tenth candidates and those preparing for TNPSC exams can check the Maths Book Back Answers PDF below. Samacheer Kalvi Class 10th Std Maths Book Back Answers Chapter 3 Exercise 3.15 Solutions are available below. Check the complete Samacheer Kalvi 10th Maths – Algebra Ex 3.15 Book Back Answers below:

We also provide class 10th other units Maths Book Back One, Two, and Five Mark Solutions Guide on our site. Students looking for the 10th standard Maths Ex 3.15 – Algebra Book Back Questions with Answer PDF

For the complete Samacheer Kalvi 10th Maths Book Back Solutions Guide PDF, check the link – Samacheer Kalvi 10th Maths Book Back Answers

Samacheer Kalvi 10th Maths Book Back Answers – Ex 3.15 Algebra

Samacheer Kalvi 10th Maths Book Subject One Mark, Two Mark, Five Mark Guide questions and answers are below. Check Maths Book Back Questions with Answers. Take the printout and use it for exam purposes.

For Samacheer Kalvi 10th Maths Book PDF, check the link – 10th Maths Book PDF

Chapter 3

Exercise 3.15 Algebra

1. Graph the following quadratic equations and state their nature of solutions,
(i) x² – 9x + 20 = 0
Solution:

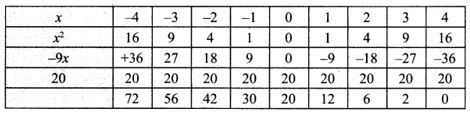
Step 1:
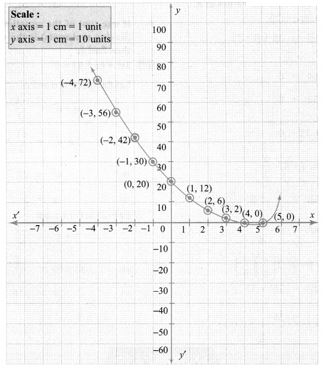
Points to be plotted : (-4, 72), (-3, 56), (-2, 42), (-1, 30), (0, 20), (1, 12), (2, 6), (3, 2), (4, 0)
Step 2:
The point of intersection of the curve with x axis is (4, 0)
Step 3:

The roots are real & unequal
∴ Solution {4, 5}

(ii) x² – 4x + 4 = 0

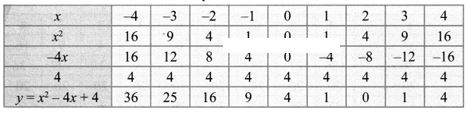
Step 1: Points to be plotted : (-4, 36), (-3, 25), (-2, 16), (-1, 9), (0, 4), (1, 1), (2, 0), (3, 1), (4, 4)
Step 2: The point of intersection of the curve with x axis is (2, 0)
Step 3:

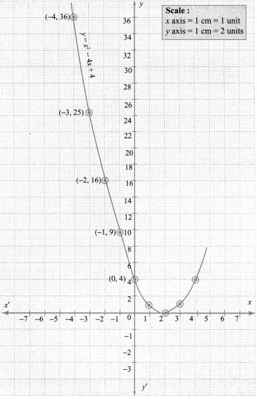
Since there is only one point of intersection with x axis, the quadratic equation x² – 4x + 4 = 0 has real and equal roots.
∴ Solution{2, 2}

(iii) x² + x + 7 = 0
Let y = x² + x + 7
Step 1:

Step 2:
Points to be plotted: (-4, 19), (-3, 13), (-2, 9), (-1, 7), (0, 7), (1, 9), (2, 13), (3, 19), (4, 27)
Step 3:
Draw the parabola and mark the co-ordinates of the parabola which intersect with the x-axis.

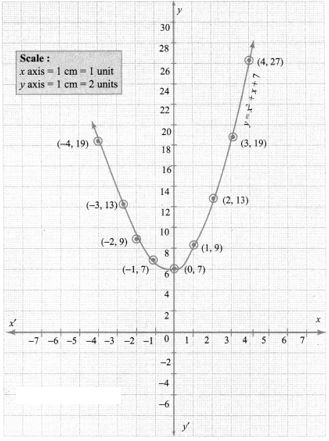
Step 4:
The roots of the equation are the points of intersection of the parabola with the x axis. Here the parabola does not intersect the x axis at any point.
So, we conclude that there is no real roots for the given quadratic equation,

(iv) x² – 9 = 0
Let y = x² – 9
Step 1:

Step 2:
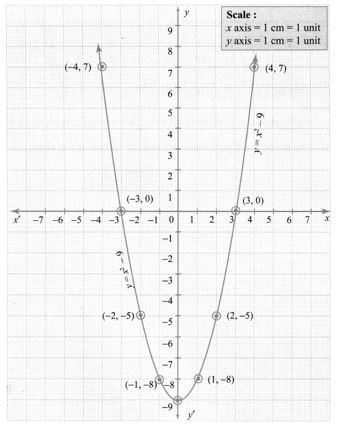
The points to be plotted: (-4, 7), (-3, 0), (-2, -5), (-1, -8), (0, -9), (1,-8), (2, -5), (3, 0), (4, 7)
Step 3:
Draw the parabola and mark the co-ordinates of the parabola which intersect the x-axis.

Step 4:
The roots of the equation are the co-ordinates of the intersecting points (-3, 0) and (3, 0) of the parabola with the x-axis which are -3 and 3 respectively.
Step 5:
Since there are two points of intersection with the x axis, the quadratic equation has real and unequal roots.
∴ Solution{-3, 3}

 

(v) x² – 6x + 9 = 0
Let y = x² – 6x + 9
Step 1:

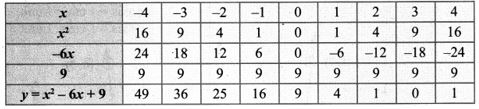
Step 2:
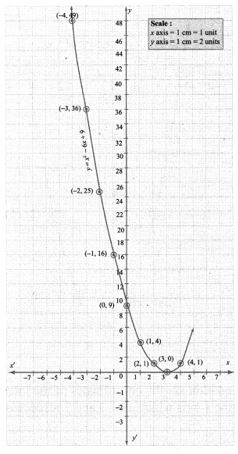
Points to be plotted: (-4, 49), (-3, 36), (-2, 25), (-1, 16), (0, 9), (1, 4), (2, 1), (3, 0), (4, 1)
Step 3:
Draw the parabola and mark the co-ordinates of the intersecting points.

Step 4:
The point of intersection of the parabola with x axis is (3, 0)
Since there is only one point of intersection with the x-axis, the quadratic equation has real and equal roots. .
∴ Solution (3, 3)

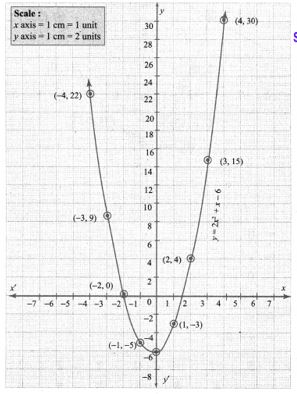
(vi) (2x – 3)(x + 2) = 0
2x² – 3x + 4x – 6 = 0
2x² + 1x – 6 = 0
Let y = 2x² + x – 6 = 0
Step 1:

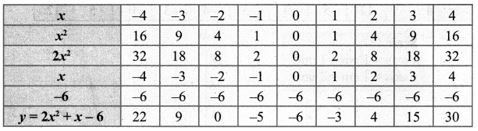
Step 2:
The points to be plotted: (-4, 22), (-3, 9), (-2, 0), (-1, -5), (0, -6), (1, -3), (2, 4), (3, 15), (4, 30)
Step 3:
Draw the parabola and mark the co-ordinates of the intersecting point of the parabola with the x-axis.

Step 4:
The points of intersection of the parabola with the x-axis are (-2, 0) and (1.5, 0).
Since the parabola intersects the x-axis at two points, the, equation has real and unequal roots.
∴ Solution {-2, 1.5}

 

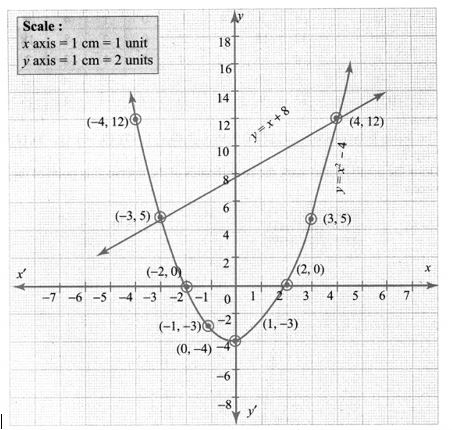
2. Draw the graph of y = x² – 4 and hence solve x² – x – 12 = 0
Solution:

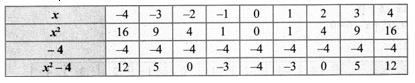
Point of intersection (-3, 5), (4, 12) solution of x² – x – 12 = 0 is -3, 4

3. Draw the graph of y = x² + x and hence solve x² + 1 = 0.
Solution:

Draw the parabola by the plotting the points (-4, 12), (-3, 6), (-2, 2), (-1, 0), (0, 0), (1, 2), (2, 6), (3, 12), (4, 20), (5, 30)

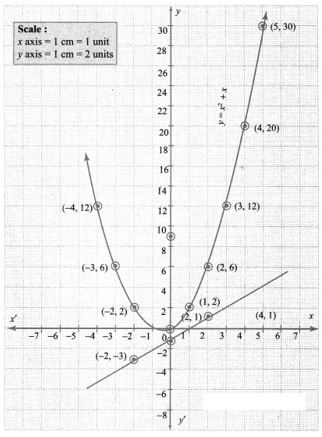
To solve: x² + 1 = 0, subtract x² + 1 = 0 from y = x² + x.
x² + 1 = 0 from y = x² + x

Plotting the points (-2, -3), (0, -1), (2, 1) we get a straight line. This line does not intersect the parabola. Therefore there is no real roots for the equation x² + 1 = 0.

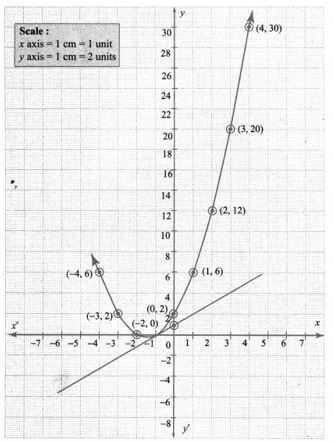
4. Draw the graph of y = x² + 3x + 2 and use it to solve x² + 2x + 1 = 0.
Solution:

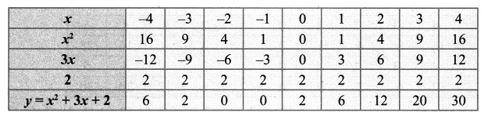
Draw the parabola by plotting the point (-4, 6), (-3, 2), (-2, 0), (-1, 0), (0, 2), (1, 6), (2, 12), (3, 20), (4, 30).

To solve x² + 2x + 1 = 0, subtract x² + 2x + 1 = 0 from y = x² + 3x + 2

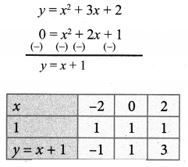
Draw the straight line by plotting the points (-2, -1), (0, 1), (2, 3)
The straight line touches the parabola at the point (-1,0)
Therefore the x coordinate -1 is the only solution of the given equation

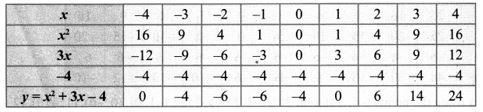
5. Draw the graph of y = x² + 3x – 4 and hence use it to solve x² + 3x – 4 = 0. y = x² + 3x – 4
Solution:

Draw the parabola using the points (-4, 0), (-3, -4), (-2, -6), (-1, -6), (0, -4), (1, 0), (2, 6), (3, 14), (4, 24).

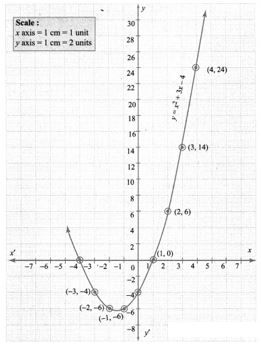
To solve: x² + 3x – 4 = 0 subtract x² + 3x – 4 = 0 from y = x² + 3x – 4 ,

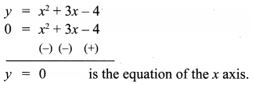
The points of intersection of the parabola with the x axis are the points (-4, 0) and (1, 0), whose x – co-ordinates (-4, 1) is the solution, set for the equation x² + 3x – 4 = 0.

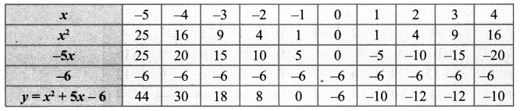
6. Draw the graph of y = x² – 5x – 6 and hence solve x² – 5x – 14 = 0.
Solution:

Draw the parabola using the points (-5, 44), (-4, 30), (-3, 18), (-2, 8), (-1, 0), (0, -6), (1, -10), (2, -12), (3, -12), (4, -10)

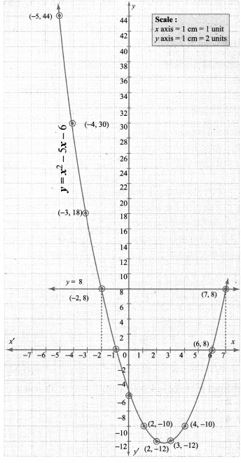
To solve the equation x² – 5x – 14 = 0, subtract x² – 5x – 14 = 0 from y = x² – 5x – 6.

The co-ordinates of the points of intersection of the line and the parabola forms the solution set for the equation x2 – 5x – 14 = 0.
∴ Solution {-2, 7}

7. Draw the graph of y = 2x² – 3x – 5 and hence solve 2x² – 4x – 6 = 0. y = 2x² – 3x – 5
Solution:

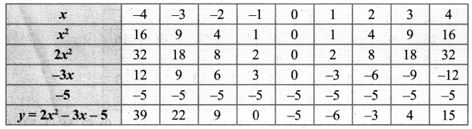
Draw the parabola using the points (-4, 39), (-3, 22), (-2, 9), (-1, 0), (0, -5), (1, -6), (2, -3), (3, 4), (4, 15).

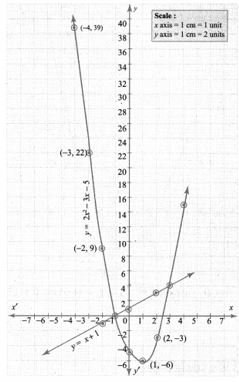
To solve 2x² – 4x – 6 = 0, subtract it from y = 2x² – 3x – 5

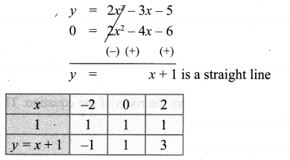
Draw a straight line using the points (-2, -1), (0, 1), (2, 3). The points of intersection of the parabola and the straight line forms the roots of the equation.
The x-coordinates of the points of intersection forms the solution set.
∴ Solution {-1, 3}

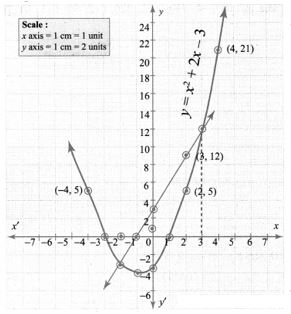
8. Draw the graph of y = (x – 1)(x + 3) and hence solve x² – x – 6 = 0.
Solution:
y = (x – 1)(x + 3) = x² – x + 3x – 3 = 0
y = x² + 2x – 3

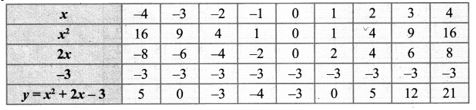
Draw the parabola using the points (-4, 5), (-3, 0), (-2, -3), (-1,-4), (0, -3), (1, 0), (2, 5), (3, 12), (4, 21)

To solve the equation x² – x – 6 = 0, subtract x² – x – 6 = 0 from y = x² – 2x – 3.

Plotting the points (-2, -3), (-1, 0), (0, 3), (2, 9), we get a straight line.
The points of intersection of the parabola with the straight line give the roots of the equation. The co¬ordinates of the points of intersection form the solution set.
∴ Solution {-2, 3}

Other Important Links for 10th Maths Book Back Answers Solutions:

For 10th Maths Chapter 3 book back question and answers, check the link – Samacheer kalvi 10th Maths Chapter 3 Algebra

Click here for the complete Samacheer Kalvi 10th Maths Book Back Solution Guide PDF – 10th Maths Book Back Answers