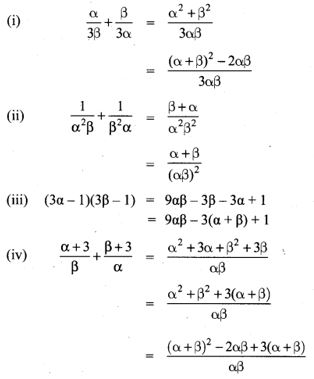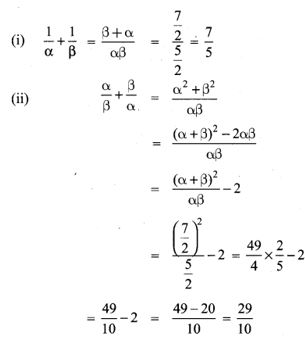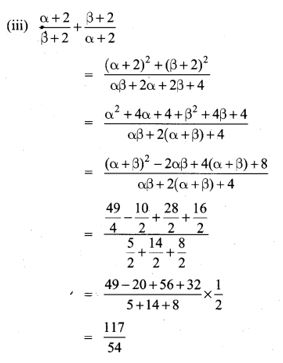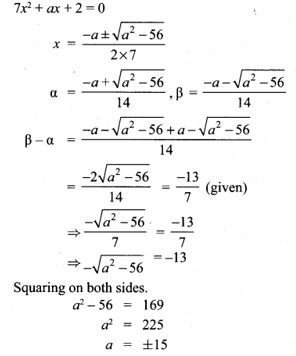10th Maths Book Back Question and Answers – Chapter 3 Exercise 3.14:

Samacheer Kalvi 10th Standard Maths Book Back Questions with Answers PDF uploaded and the same given below. Class-tenth candidates and those preparing for TNPSC exams can check the Maths Book Back Answers PDF below. Samacheer Kalvi Class 10th Std Maths Book Back Answers Chapter 3 Exercise 3.14 Solutions are available below. Check the complete Samacheer Kalvi 10th Maths – Algebra Ex 3.14 Book Back Answers below:

We also provide class 10th other units Maths Book Back One, Two, and Five Mark Solutions Guide on our site. Students looking for the 10th standard Maths Ex 3.14 – Algebra Book Back Questions with Answer PDF

For the complete Samacheer Kalvi 10th Maths Book Back Solutions Guide PDF, check the link – Samacheer Kalvi 10th Maths Book Back Answers

Samacheer Kalvi 10th Maths Book Back Answers – Ex 3.14 Algebra

Samacheer Kalvi 10th Maths Book Subject One Mark, Two Mark, Five Mark Guide questions and answers are below. Check Maths Book Back Questions with Answers. Take the printout and use it for exam purposes.

For Samacheer Kalvi 10th Maths Book PDF, check the link – 10th Maths Book PDF

Chapter 3

Exercise 3.14 Algebra

1. Write each of the following expressions in terms of α + β and αβ.

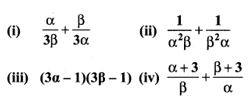
Solution:

2.The roots of the equation 2x² – 7x + 5 = 0 are α and β. Without solving the root find

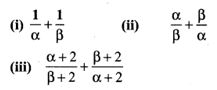
Solution:
2x² – 7x + 5 = x² – 72x+52 = 0
α + β = 72
αβ = 52

3.The roots of the equation x² + 6x – 4 = 0 are α, β. Find the quadratic equation whose roots are
(i) α² and β²
(ii) 2α and 2β
(iii) α²β and β²α
Solution:
If the roots are given, the quadratic equation is x² – (sum of the roots) x + product the roots = 0.
For the given equation.
x² + 6x – 4 = 0
α + β = -6
αβ = -4
(i) α² + β² = (α + β)² – 2αβ
= (-6)² – 2(-4) = 36 + 8 = 44
α²β² = (αβ)² = (-4)² = 16
∴ The required equation is x² – 44x – 16 = 0.

(iii) α²β + β²α = αβ(α + β)
= -4(-6) = 24
α²β × β²α = α³β³ = (αβ)³ = (-4)³ = -64
∴ The required equation = x² – 24x – 64 – 0.

4.If α, β are the roots of 7x² + ax + 2 = 0 and if β – α = −137 Find the values of a.
Solution:

5.If one root of the equation 2y² – ay + 64 = 0 is twice the other then find the values of a.
Solution:
Let one of the root α = 2β
α + β = 2β + β = 3β
Given

a² = 576
a = 24, -24

6. If one root of the equation 3x² + kx + 81 = 0 (having real roots) is the square of the other then find k.
Solution:
3x² + kx + 81 = 0
Let the roots be α and α²

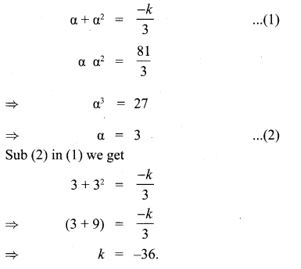
Other Important Links for 10th Maths Book Back Answers Solutions:

For 10th Maths Chapter 3 book back question and answers, check the link – Samacheer kalvi 10th Maths Chapter 3 Algebra

Click here for the complete Samacheer Kalvi 10th Maths Book Back Solution Guide PDF – 10th Maths Book Back Answers