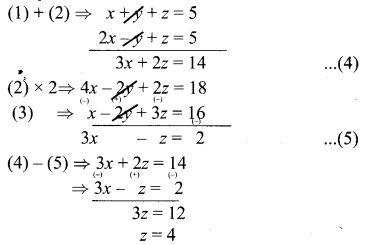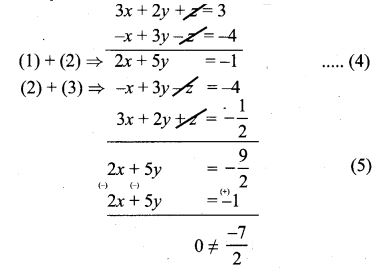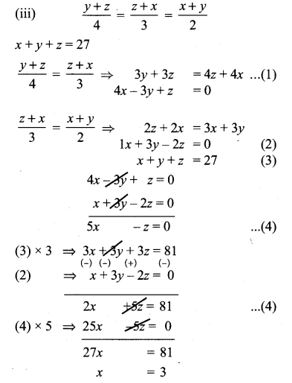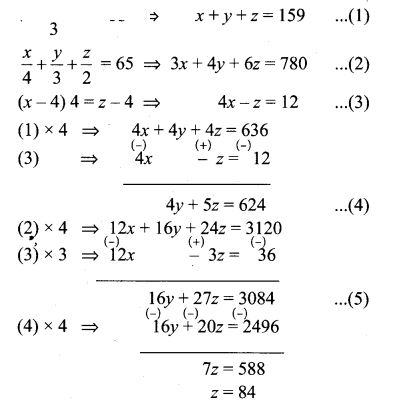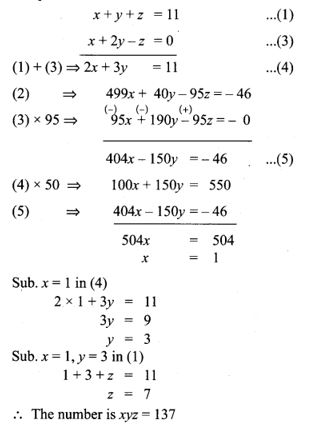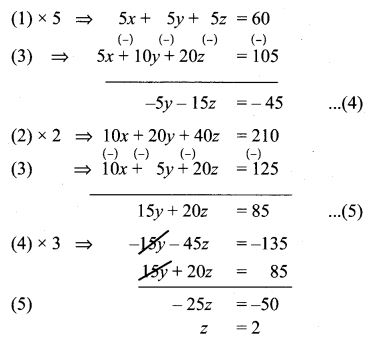10th Maths Book Back Question and Answers – Chapter 3 Exercise 3.1:
Samacheer Kalvi 10th Standard Maths Book Back Questions with Answers PDF uploaded and the same given below. Class-tenth candidates and those preparing for TNPSC exams can check the Maths Book Back Answers PDF below. Samacheer Kalvi Class 10th Std Maths Book Back Answers Chapter 3 Exercise 3.1 Solutions are available below. Check the complete Samacheer Kalvi 10th Maths – Algebra Ex 3.1 Book Back Answers below:
We also provide class 10th other units Maths Book Back One, Two, and Five Mark Solutions Guide on our site. Students looking for the 10th standard Maths Ex 3.1 – Algebra Book Back Questions with Answer PDF
For the complete Samacheer Kalvi 10th Maths Book Back Solutions Guide PDF, check the link – Samacheer Kalvi 10th Maths Book Back Answers
Samacheer Kalvi 10th Maths Book Back Answers – Ex 3.1 Algebra
Samacheer Kalvi 10th Maths Book Subject One Mark, Two Mark, Five Mark Guide questions and answers are below. Check Maths Book Back Questions with Answers. Take the printout and use it for exam purposes.
For Samacheer Kalvi 10th Maths Book PDF, check the link – 10th Maths Book PDF
Chapter 3
Exercise 3.1 Algebra
1. Solve the following system of linear equations in three variables
(i) x + y + z = 5; 2x – y + z = 9; x – 2y + 3z = 16
(ii) 1x – 2y + 4 = 0; 1y – 1z + 1 = 0; 2z + 3x = 14
(iii) x + 20 = 3y2 + 10 = 2z + 5 = 110 – (y + z)
Solutions:
(i) x + y + z = 5 ………….. (1)
2x – y + z = 9 …………. (2)
x – 2y + 3z = 16 …………. (3)
Substitute z = 4 in (4)
3x + 2(4) = 14
3x + 8 = 14
3x = 6
x = 2
Substitute x = 2, z = 4 in (1)
2 + y + 4 = 5 ⇒ y = -1
x = 2, y = -1, z = 4
(iii) x + 20 = 3y2 + 10 = 2z + 5 = 110 – (y + z)
x = 3y2 – 10 …………. (1)
2z + 5 = 110 – (y + z)
2z = 105 – y – z
y = 105 – 3z ………….. (2)
Substitute (2) in (1), x = 3152 – 9z2 – 10
= 2z + 5 – 20
∴ 315 – 9z – 20 = 4z – 30
13 z = 315 – 20 + 30
= 325
z = 32513 = 25
x + 20 = 2z + 5
x + 20 = 50 + 5
x = 35
Substitute z = 25 in (2)
y = 105 – 3z = 105 – 75 = 30
y = 30
x = 35, y = 30, z = 25
The system has unique solutions.
2. Discuss the nature of solutions of the following system of equations
(i) x + 2y – z = 6 ; -3x – 2y + 5z = -12 ; x – 2z = 3
(ii) 2y + z = 3 (-x + 1); -x + 3y -z = -4 3x + 2y + z = – 12
(iii) y+z4 = z+x3 = x+y2; x + y + z = 27
Solution:
(i) x + 2y – z = 6 …………. (1)
-3x – 2y + 5z = -12 ……… (2)
x – 2z = 3 …………… (3)
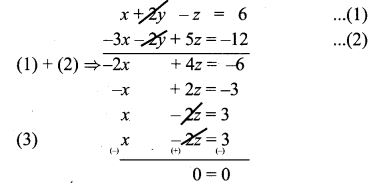
We see that the system has an infinite number of solutions.
(ii) 2y + z = 3(-x + 1);
-x + 3y – z = -4;
3x + 2y + z = –12
2y + z + 3x = 3 ⇒ 3x + 2y + z = 3 ………….. (1)
-x + 3y – z = -4 …………. (2)
3x + 2y + z = –12 ………………. (3)
This is a contradiction. This means the system is inconsistent and has no solutions.
Sub. x = 3 in (4) ⇒ 5(3) – z = 0
15 – z = 0
-z = -15
z = 15
Sub, x = 3, z = 15 in (3)
x + y + z = 27
3 + y + 15 = 27
y = 27 – 18 = 9
x = 3, y = 9, z = 15
∴ The system has unique solutions.
3. Vani, her father, and her grandfather have an average age of 53. One-half of her grandfather’s age plus one-third of her father’s age plus one-fourth of Vani’s age is 65. Four years ago if Vani’s grandfather was four times as old as Vani then how old are they all now?
Solution:
Let Vani’s age be x
Let Vani’s father’s age be y
Let Vani’s grandfather’s age be z.
Sub, z = 84 in (3), we get
4x – 84 = 12
4x = 96
x = 24
Sub, x = 24, z = 84 in (1) we get
24 + y + 84 = 159
y = 159 – 108
= 51
∴ Vani’s age = 24 years
Her father’s age =51 years
Her grand father’s age = 84 years.
4. The sum of the digits of a three-digit number is 11. If the digits are reversed, the new number is 46 more than five times the former number. If the hundreds digit plus twice the tens digit is equal to the units digit, then find the original three digit number?
Solution:
Let the number be 100x + 10y + z.
Reversed number be 100z + 10y + x.
x + y + z = 11 …………… (1)
100z + 10y + x = 5(100x + 10y + z) + 46
100z + 10y + x = 500x + 50y + 5z + 46
499x + 40y – 95z -46 ………….. (2)
x + 2y = z
x + 2y – z = 0 ……………. (3)
5. There are 12 pieces of five, ten, and twenty rupee currencies whose total value is ₹105. When the first 2 sorts are interchanged in their numbers its value will be increased by ₹20. Find the number of currencies in each sort.
Solution:
Let x, y and z be number of currency pieces of 5,10,20 rupees
x + y + z = 12 ………. (1)
5x + 10y + 20z = 105 ………… (2)
10x + 5y + 20z = 125 …………. (3)
Sub, z = 2 in (5), we get
15y + 20 × 2 = 85
15y = 45
y = 3
Sub; y = 3, z = 2 in (1)
x + y + z = 12
x = 7
∴ The solutions are
the number of ₹ 5 are 7
the number of ₹ 10 are 3
the number of ₹ 20 are 2
Other Important Links for 10th Maths Book Back Answers Solutions:
For 10th Maths Chapter 3 book back question and answers, check the link – Samacheer kalvi 10th Maths Chapter 3 Algebra
Click here for the complete Samacheer Kalvi 10th Maths Book Back Solution Guide PDF – 10th Maths Book Back Answers