Samacheer kalvi 10th Maths - Statistics and Probability Ex 8.4

10th Maths Book Back Question and Answers – Chapter 8 Exercise 8.4:

Samacheer Kalvi 10th Standard Maths Book Back Questions with Answers PDF uploaded and the same given below. Class-tenth candidates and those preparing for TNPSC exams can check the Maths Book Back Answers PDF below. Samacheer Kalvi Class 10th Std Maths Book Back Answers Chapter 8 Statistics and Probability Exercise 8.4 Solutions are available below. Check the complete Samacheer Kalvi 10th Maths – Statistics and Probability Ex 8.4 Book Back Answers below:

We also provide class 10th other units Maths Book Back One, Two, and Five Mark Solutions Guide on our site. Students looking for the 10th standard Maths Ex 8.4 – Statistics and Probability Book Back Questions with Answer PDF

For the complete Samacheer Kalvi 10th Maths Book Back Solutions Guide PDF, check the link – Samacheer Kalvi 10th Maths Book Back Answers

Samacheer Kalvi 10th Maths Book Back Answers – Ex 8.4 Statistics and Probability

Samacheer Kalvi 10th Maths Book Subject One Mark, Two Mark, Five Mark Guide questions and answers are below. Check Maths Book Back Questions with Answers. Take the printout and use it for exam purposes.

For Samacheer Kalvi 10th Maths Book PDF, check the link – 10th Maths Book PDF

Chapter 8 Exercise 8.4 Statistics and Probability

1. If P(A) = \(\frac{2}{3}\), P(B) = \(\frac{2}{5}\), P(A∪B) = 13 then find P(A∩B).
Solution:
P(A) = \(\frac{2}{3}\), P(B) = \(\frac{2}{5}\), P(A∪B) = \(\frac{1}{3}\)
P(A ∩ B) = P(A) + P(B) – P(A∪B)

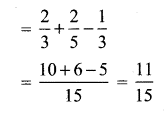
2. A and B are two events such that, P(A) = 0.42, P(B) = 0.48, and P(A ∩ B) = 0.16. Find
(i) P(not A)
(it) P(not B)
(iii) P(A or B)
Answer:
(i) P(not A) = 1 – P (A) = 1 – 0.42 = 0.58
(ii) P(not B) = 1 – P(B) = 1 – 0.48 = 0.52
(iii) P(A or B) = P(A) + P(B) – P(A ∩ B) = 0.42 + 0.48 – 0.16 = 0.90 – 0.16 = 0.74

3. If A and B are two mutually exclusive events of a random experiment and P(not A) = 0.45, P(A∪B) = 0.65, then find P(B).
Solution:
A and B are two mutually exclusive events of a random experiment.
P(not A) = 0.45,
P(A) = 1 – P(not A)
P(A∪B) = 0.65 = 1 – 0.45 = 0.55
P(A∪B) = P(A) + P(B) = 0.65
0.55 + P(B) = 0.65
P(B) = 0.65 – 0.55
= 0.10

4. The probability that atleast one of A and B occur is 0.6. If A and B occur simultaneously with probability 0.2, then find P(\(\bar{A}\)) + P(\(\bar{B}\)).
Answer:
Here P (A ∪ B) = 0.6, P (A ∩ B) = 0.2
P (A ∪ B) = P (A) + P (B) – P (A ∩ B)
0.6 = P (A) + P (B) – 0.2
P(A) + P(B) = 0.8
P(\(\bar{A}\)) + P(\(\bar{B}\)) = 1 – P(A) + 1 – P(B)
= 2 – [P(A) + P(B)]
= 2 – 0.8
= 1.2

5. The probability of happening of an event A is 0.5 and that of B is 0.3. If A and B are mutually exclusive events, then find the probability that neither A nor B happen.
Solution:
P(A) = 0.5 Since A and B are mutually inclusive events
P(B) = 0.3 events.
P(\(\overline{\mathbf{A}}\))∪P(\(\overline{\mathbf{B}}\)) = 1 – [P(A) + P(B)]
= 1 – [0.5 + 0.3] = 0.2

6. Two dice are rolled once. Find the probability of getting an even number on the first die or a total of face sum 8.
Solution:
Two dice rolled once.

7. From a well-shuffled pack of 52 cards, a card is drawn at random. Find the probability of it being either a red king or a black queen.
Solution:
n(S) = 52
No. of Red cards = 26,
Red king cards = 2
No. of Black cards = 26,
Black queen cards = 2
No. of red king cards = n(K) = 2

∴ The probability of being either a red king or a black queen = \(\frac{1}{13}\).

8. A box contains cards numbered 3, 5, 7, 9,… 35, 37. A card is drawn at random from the box. Find the probability that the drawn card has either multiples of 7 or a prime number.
Solution:
S = {3, 5, 7, 9, 11, 13, 15, 17, 19, 21, 23, 25, 27, 29, 31, 33, 35, 37}
n(S) = 18
Multiplies of seven cards (A) = {7, 21, 35}
= n(A) = 3

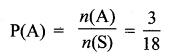
Let the prime number cards B
B = {3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37}
n(B) = 11

9. Three unbiased coins are tossed once. Find the probability of getting at most 2 tails or at least 2 heads.
Solution:
When we toss three coins, the sample space S = {HHH, TTT, HTT, THH, HHT, TTH, HTH, THT}
n(S) = 8
Event of getting at most 2 tails be A.
∴ A = { HHH, HTT, THH, HHT, TTH, HTH, THT}

10. The probability that a person will get an electrification contract is a probability that he will not get a plumbing contract is \(\frac{3}{5}\). The probability of getting at least one contract is \(\frac{5}{8}\). What is the probability that he will get both?
Solution:

12. A coin is tossed thrice. Find the probability of getting exactly two heads or at least one tail or two consecutive heads.
Solution:
Three coins tossed simultaneously.
S = { HHH, TTT, HHT, TTH, HTH, THT, HTT, THH}
n(S) = 8
Happening of getting exactly two heads be A.
A= {HHT, HTH, THH}
n(A) = 3

Event of getting at least one tail be B.
∴ B = {TTT, HHT, TTH, HTH, THT, HTT, THH}

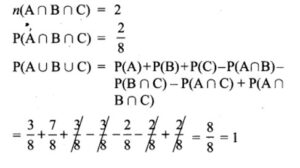
13. If A, B, C are any three events such that probability of B is twice as that of probability of A and probability of C is thrice as that of probability of A and if P(A∩B) = \(\frac{1}{6}\), P(B∩C) = \(\frac{1}{4}\), P(A∩C) = \(\frac{1}{8}\), \(\mathbf{P}(\mathbf{A} \cup \mathbf{B} \cup \mathbf{C})=\frac{9}{10}, \mathbf{P}(\mathbf{A} \cap \mathbf{B} \cap \mathbf{C})=\frac{1}{15}\), then find P(A), P(B) and P(C)?
Solution:
P(B) = 2P(A)
P(C) = 3P(A)

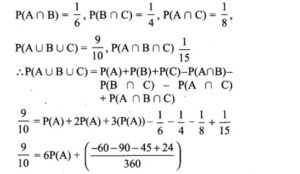
14. In a class of 35, students are numbered from 1 to 35. The ratio of boys to girls is 4:3. The roll numbers of students begin with boys and end with girls. Find the probability that a student selected is either a boy with a prime roll number or a girl with a composite roll number or an even roll number.
Solution:

How To Get Govt. Job Without Wasting Years?
CLICK HERE

07 Apr 2022