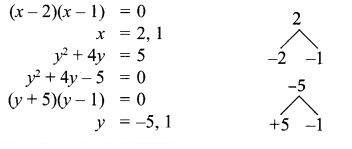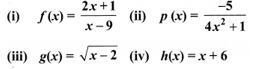Samacheer kalvi 10th Maths - Relations and Functions Ex 1.6

10th Maths Book Back Question and Answers – Chapter 1 Exercise 1.6:

Samacheer Kalvi 10th Standard Maths Book Back Questions with Answers PDF uploaded and the same given below. Class-tenth candidates and those preparing for TNPSC exams can check the Maths Book Back Answers PDF below. Samacheer Kalvi Class 10th Std Maths Book Back Answers Chapter 1 Exercise 1.6 Solutions are available below. Check the complete Samacheer Kalvi 10th Maths – Relations and Functions Ex 1.6 Book Back Answers below:

We also provide class 10th other units Maths Book Back One and Two Mark Solutions Guide on our site. Students looking for the 10th standard Maths Ex 1.6 – Relations and Functions Book Back Questions with Answer PDF

For the complete Samacheer Kalvi 10th Maths Book Back Solutions Guide PDF, check the link – Samacheer Kalvi 10th Maths Book Back Answers

Samacheer Kalvi 10th Maths Book Back Answers – Ex 1.6 Relations and Functions

Samacheer Kalvi 10th Maths Book Subject One Mark, Two Mark, Five Mark Guide questions and answers are below. Check Maths Book Back Questions with Answers. Take the printout and use it for exam purposes.

For Samacheer Kalvi 10th Maths Book PDF, check the link – 10th Maths Book PDF

Chapter 1 Ex 1.6 Relations and Functions

1.If n(A × B) = 6 and A = {1, 3} then n(B) is
(1) 1
(2) 2
(3) 3
(4) 6
Solu.:
(3) 3
Hint:
If n(A × B) = 6
A = {1, 1}, n(A) = 2
n(B) = 3

2.A = {a, b,p}, B = {2, 3}, C = {p, q, r, s)
then n[(A ∪ C) × B] is ………….
(1) 8
(2) 20
(3) 12
(4) 16
Solu.:
(3) 12
Hint: A ∪ C = [a, b, p] ∪ [p, q, r, s]
= [a, b, p, q, r, s]
n (A ∪ C) = 6
n(B) = 2
∴ n [(A ∪ C)] × B] = 6 × 2 = 12

3.If A = {1, 2}, B = {1, 2, 3, 4}, C = {5, 6} and D = {5, 6, 7, 8} then state which of the following statement is true.
(1) (A × C) ⊂ (B × D)
(2) (B × D) ⊂ (A × C)
(3) (A × B) ⊂ (A × D)
(4) (D × A) ⊂ (B × A)
Solu.:
(1) (A × C) ⊂ (B × D)]
Hint:
A = {1, 2}, B = {1, 2, 3, 4},
C = {5, 6}, D ={5, 6, 7, 8}
A × C ={(1,5), (1,6), (2, 5), (2, 6)}
B × D = {(1, 5),(1, 6),(1, 7),(1, 8),(2, 5),(2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8)}
∴ (A × C) ⊂ B × D it is true

4. If there are 1024 relations from a set A = {1, 2, 3, 4, 5} to a set B, then the number of elements in B is ………………….
(1) 3
(2) 2
(3) 4
(4) 8
Solu.:
(2) 2
Hint: n(A) = 5
n(A × B) = 10
(consider 1024 as 10)
n(A) × n(B) = 10
5 × n(B) = 10
n(B) = 105 = 2
n(B) = 2

5. The range of the relation R = {(x, x²)|x is a prime number less than 13} is
(1) {2, 3, 5, 7}
(2) {2, 3, 5, 7, 11}
(3) {4, 9, 25, 49, 121}
(4) {1, 4, 9, 25, 49, 121}
Solu.:
(3) {4, 9, 25, 49, 121}]
Hint:
R = {(x, x²)/x is a prime number < 13}
The squares of 2, 3, 5, 7, 11 are
{4, 9, 25, 49, 121}

6. If the ordered pairs (a + 2,4) and (5, 2a + 6) are equal then (a, b) is ………
(1) (2, -2)
(2) (5, 1)
(3) (2, 3)
(4) (3, -2)
Solu.:
(4) (3, -2)
Hint:

The value of a = 3 and b = -2

7. Let n(A) = m and n(B) = n then the total number of non-empty relations that can be defined from A to B is
(1) mⁿ
(2) n^m
(3) 2^mn– 1
(4) 2^mn
Solu.:
(4) 2^mn
Hint:
n(A) = m, n(B) = n
n(A × B) = 2^mn

8. If {(a, 8),(6, b)} represents an identity function, then the value of a and 6 are respectively
(1) (8,6)
(2) (8,8)
(3) (6,8)
(4) (6,6)
Solu.:
(1) (8,6)
Hint: f = {{a, 8) (6, 6)}. In an identity function each one is the image of it self.
∴ a = 8, b = 6

9. Let A = {1, 2, 3, 4} and B = {4, 8, 9, 10}. A function f : A → B given by f = {(1, 4),(2, 8),(3, 9),(4, 10)} is a
(1) Many-one function
(2) Identity function
(3) One-to-one function
(4) Into function
Solu.:
(3) One-to one function
Hint:
A = {1, 2, 3, 4), B = {4, 8, 9,10}

10. If f(x) = 2x² and g (x) = 13x, Then fog is

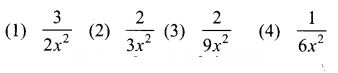
Solu.:
(3) 29×2
Hint:
f(x) = 2x²
g(x) = 13x
fog = f(g(x)) = f(13x)=2(13x)2
= 2 × 19×2=29×2

11. If f: A → B is a bijective function and if n(B) = 7, then n(A) is equal to …………..
(1) 7
(2) 49
(3) 1
(4) 14
Solu.:
(1) 7
Hint:
n(B) = 7
Since it is a bijective function, the function is one – one and also it is onto.
n(A) = n(B)
∴ n(A) = 7

12. Let f and g be two functions given by f = {(0, 1), (2, 0), (3, -4), (4, 2), (5, 7)} g = {(0, 2), (1, 0), (2, 4), (-4, 2), (7, 0)} then the range of fog is
(1) {0, 2, 3, 4, 5}
(2) {-4, 1, 0, 2, 7}
(3) {1, 2, 3, 4, 5}
(4) {0, 1, 2}
Solu.:
(4) {0, 1, 2}
Hint:
gof = g(f(x))
fog = f(g(x))
= {(0, 2),(1, 0),(2, 4),(-4, 2),(7, 0)}
Range of fog = {0, 1, 2}

13. Let f (x) = 1+x2−−−−−√ then ………………..
(1) f(xy) = f(x) f(y)
(2) f(xy) > f(x).f(y)
(3) f(xy) < f(x). f(y)
(4) None of these
Solu.:
(3) f(xy) < f(x) . f(y)

14. If g = {(1, 1),(2, 3),(3, 5),(4, 7)} is a function given by g(x) = αx + β then the values of α and β are
(1) (-1, 2)
(2) (2, -1)
(3) (-1, -2)
(4) (1, 2)
Solu.:
(2) (2,-1)
Hint:
g(x) = αx + β
α = 2
β = -1
g(x) = 2x – 1
g(1) = 2(1) – 1 = 1
g(2) = 2(2) – 1 = 3
g(3) = 2(3) – 1 = 5
g(4) = 2(4) – 1 = 7

15. f(x) = (x + 1)³ – (x – 1)³ represents a function which is …………….
(1) linear
(2) cubic
(3) reciprocal
(4) quadratic
Solu.:
(4) quadratic
Hint: f(x) = (x + 1)³ – (x – 1)³
[using a³ – b³ = (a – b)³ + 3 ab (a – b)]
= (x + 1 – x + 1)³ + 3(x + 1) (x – 1)
(x + 1 – x + 1)
= 8 + 3 (x² – 1)²
= 8 + 6 (x² – 1)
= 8 + 6x² – 6
= 6x² + 2
It is quadratic polynomial

Chapter 1

Exercise 1 Relations and Functions Unit

If the ordered pairs (x² – 3x, y² + 4y) and (-2, 5) are equal, then find x and y.
Solu.:
(x² – 3x, y²+ 4y) = (-2, 5)
x² – 3x = -2
x² – 3x + 2 = 0

2. The cartesian product A × A has 9 elements among which (-1, 0) and (0,1) are found. Find the set A and the remaining elements of A × A.
Solu.:
n(A × A) = 9
n(A) = 3
A = {-1,0,1}
A × A = {-1, 0, 1} × {-1, 0, 1}
A × A = {(-1,-1)(-1, 0) (-1, 1)
(0, -1) (0, 0) (0, 1)
(1,-1) (1, 0) (1, 1)}
The remaining elements of A × A =
{(-1, -1) (-1, 1) (0, -1) (0, 0) (1,-1) (1,0) (1,1)}

3. Given that

(i) f(0)
(ii) f(3)
(iii) f(a + 1) in terms of a.(Given that a > 0)
Solu.:
(i) f(0) = 4
(ii) f(3) = 3−1−−−−√=2–√
(iii) f(a + 1) = a+1−1−−−−−−−−√=a−−√

4. Let A = {9,10,11,12,13,14,15,16,17} and let f : A → N be defined by f(n) = the highest prime factor of n ∈ A. Write f as a set of ordered pairs and find the range of f.
Solu.:
A= {9, 10, 11, 12, 13, 14, 15, 16, 17}
f: A → N
f(x) = the highest prime factor n ∈ A
f = {(9, 3) (10, 5) (11, 11) (12, 3) (13, 13) (14, 7) (15, 5) (16, 2) (17, 17)}
Range of f = {3, 5, 11, 13, 7, 2, 17}
= {2, 3, 5, 7, 11, 13, 17}

5. Find the domain of the function f(x) = 1+1−1−x2−−−−−√−−−−−−−−−−√−−−−−−−−−−−−−−−√
Solu.:
f(x) = 1+1−1−x2−−−−−√−−−−−−−−−−√−−−−−−−−−−−−−−−√
Domain of f(x) = {-1, 0, 1}
(x² = 1, -1, 0, because 1−x2−−−−−√ should be +ve, or 0)

6. If f (x) = x², g(x) = 3x and h(x) = x – 2, Prove that (f o g)o h = f o(g o h).
Solu.:
f(x) = x² ; g(x) = 3x and h(x) = x – 2
L.H.S. = (fog) oh
fog = f[g(x)]
= f(3x)
= (3x)² = 9x²
(fog) oh = fog[h(x)]
= fog (x – 2)
= 9(x – 2)²
= 9[x² – 4x + 4]
= 9x² – 36x + 36 ….(1)
R.H.S. = fo(goh)
goh = g [h(x)]
= g(x – 2)
= 3(x – 2)
= 3x – 6
fo(goh) = fo [goh (x)]
= f(3x – 6)
= (3x – 6)²
= 9x² – 36x + 36 ….(2)
From (1) and (2) we get
L.H.S. = R.H.S.
(fog) oh = fo {goh)

7. A = {1, 2} and B = {1, 2, 3, 4} , C = {5, 6} and D = {5, 6, 7, 8} . Verify whether A × C is a subset of B × D?
Solu.:
A = {1, 2), B = (1, 2, 3, 4)
C = {5, 6}, D = {5, 6, 7, 8)
A × C = {(1, 5), (1, 6), (2, 5), (2, 6)}
B × D = {(1, 5), (1, 6), (1, 7), (1, 8), (2, 5), (2, 6), (2, 7), (2, 8), (3, 5), (3, 6), (3, 7), (3, 8), (4, 5), (4, 6), (4, 7), (4, 8)}
(A × C) ⊂ (B × D) It is proved.

8. If f(x) = x−1x+1, x ≠ 1 show that f(f(x)) = −1x, Provided x ≠ 0.
Solu.:

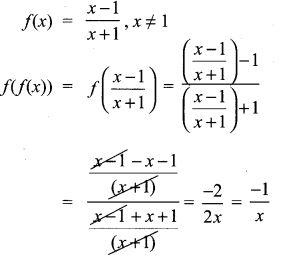
Hence it is proved.

9. The function/and g are defined by f(x) = 6x + 8; g(x) = x−23.
(i) Calculate the value of gg(12)
(ii) Write an expression for g f(x) in its simplest form.
Solu.:

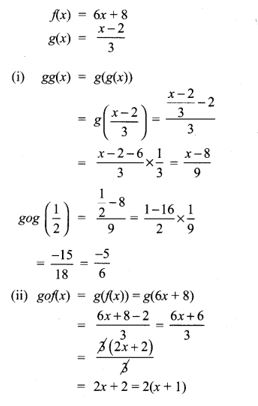
10. Write the domain of the following real functions

Solu.:
(i) f(x) = 2x+1x−9
The denominator should not be zero as the function is a real function.
∴ The domain = R – {9}
(ii) p(x) = −54×2+1
The domain is R.
(iii) g(x) = x−2−−−−−√
The domain = [2, ∝)
(iv) h(x) = x + 6
The domain is R.

How To Get Govt. Job Without Wasting Years?
CLICK HERE

01 Apr 2022