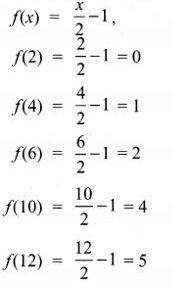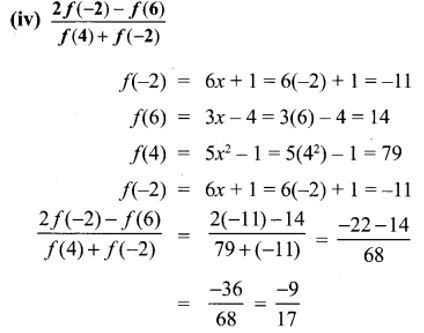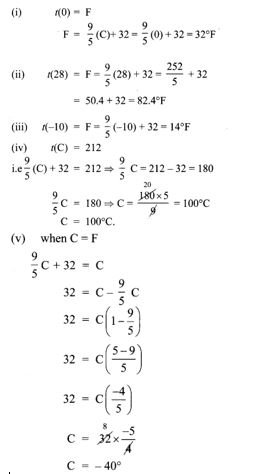10th Maths Book Back Question and Answers – Exercise 1.4:
Samacheer Kalvi 10th Standard Maths Book Back Questions with Answers PDF uploaded and the same given below. Class-tenth candidates and those preparing for TNPSC exams can check the Maths Book Back Answers PDF below. Samacheer Kalvi Class 10th Std Maths Book Back Answers Chapter 1 Exercise 1.4 Solutions are available below. Check the complete Samacheer Kalvi 10th Maths – Relations and Functions Ex 1.4 Book Back Answers below:
We also provide class 10th other chapters Maths Book Back One and Two Mark Solutions Guide on our site. Students looking for the 10th standard Maths – Relations and Functions Ex 1.4 Book Back Questions with Answer PDF
For the complete Samacheer Kalvi 10th Maths Book Back Solutions Guide PDF, check the link – Samacheer Kalvi 10th Maths Book Back Answers
Samacheer Kalvi 10th Maths Book Back Answers – Ex 1.1 Relations and Functions
Samacheer Kalvi 10th Maths Book Subject One Mark, Two Mark, Five Mark Guide questions and answers are below. Check Maths Book Back Questions with Answers. Take the printout and use it for exam purposes.
For Samacheer Kalvi 10th Maths Book PDF, check the link – 10th Maths Book PDF
Chapter 1
Exercise 1.4 Relations and Functions
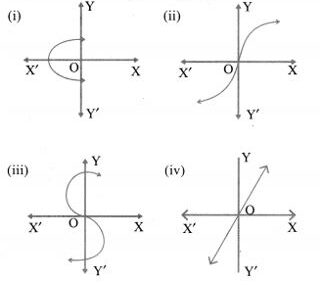
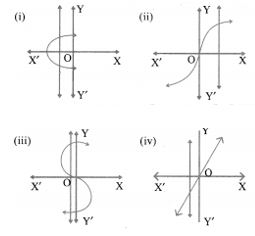
1. Determine whether the graph given below represents functions. Give a reason for your answers concerning each graph.
Solu.:
(i) It is not a function. The graph meets the vertical line at more than one point.
(ii) It is a function as the curve meets the vertical line at only one point.
(iii) It is not a function as it meets the vertical line at more than one point.
(iv) It is a function as it meets the vertical line at only one point.
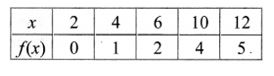
2. Let f :A → B be a function defined by f(x) = x2 – 1, Where A = {2, 4, 6, 10, 12},
B = {0, 1, 2, 4, 5, 9}. Represent f by
(i) set of ordered pairs;
(ii) a table;
(iii) an arrow diagram;
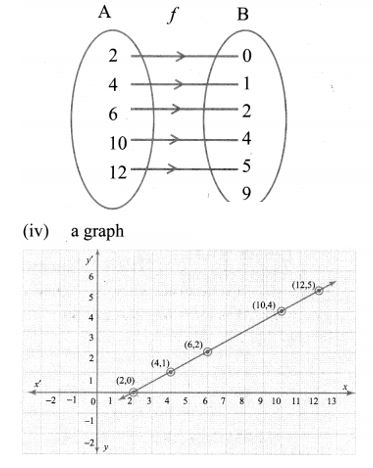
(iv) a graph
Solu.:
f: A → B
A = {2, 4, 6, 10, 12}, B = {0, 1, 2, 4, 5, 9}
(i) Set of ordered pairs
= {(2, 0), (4, 1), (6, 2), (10, 4), (12, 5)}
(ii) a table
(iii) an arrow diagram;
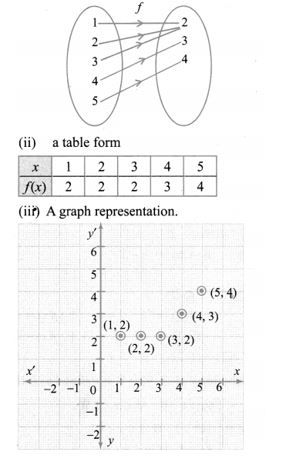
3. Represent the function f = {(1, 2),(2, 2),(3, 2), (4,3), (5,4)} through
(i) an arrow diagram
(ii) a table form
(iii) a graph
Solu.:
f = {(1, 2), (2, 2), (3, 2), (4, 3), (5, 4)}
(i) An arrow diagram.
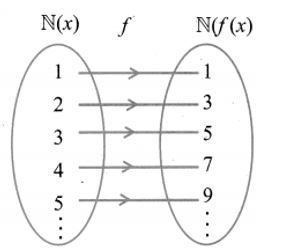
4. Show that the function f: N → N defined by f{x) = 2x – 1 is one – one but not onto.
Solu.:
f: N → N
f(x) = 2x – 1
N = {1, 2, 3, 4, 5,…}
f(1) = 2(1) – 1 = 1
f(2) = 2(2) – 1 = 3
f(3) = 2(3) – 1 = 5
f(4) = 2(4) – 1 = 7
f(5) = 2(5) – 1 = 9
In the figure, for different elements in x, there are different images in f(x).
Hence f : N → N is a one-one function.
A function f: N → N is said to be onto function if the range of f is equal to the co-domain of f
Range = {1, 3, 5, 7, 9,…}
Co-domain = {1, 2, 3,..}
But here the range is not equal to co-domain. Therefore it is one-one but not onto function.
5.Show that the function f: N → N defined by f (m) = m2 + m + 3 is one – one function.
Solution:
f: N → N
f(m) = m2 + m + 3
N = {1, 2, 3, 4, 5…..}m ∈ N
f{m) = m2 + m + 3
f(1) = 12 + 1 + 3 = 5
f(2) = 22 + 2 + 3 = 9
f(3) = 32 + 3 + 3 = 15
f(4) = 42 + 4 + 3 = 23
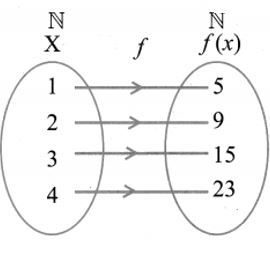
In the figure, for different elements in the (X) domain, there are different images in f(x). Hence f: N → N is one-to-one but not onto function as the range of f is not equal to the co-domain.
Hence it is proved.
6. Let A = {1,2, 3, 4} and B = N .
Let f: A → B be defined by f(x) = x3 then,
(i) find the range of f
(ii) identify the type of function
Solu.:
A = {1,2, 3,4}
B = {1,2, 3, 4, 5,….}
f(x) = x3
f(1) = 13 = 1
f(2) = 23 = 8
f(3) = 33 = 27
f(4) = 43 = 64
(i) Range = {1,8, 27, 64}
(ii) one -one and into function.
7. In each of the following cases state whether the function is bijective or not. Justify your answer.
(i) f: R → R defined by f(x) = 2x + 1
(ii) f: R → R defined by f(x) = 3 – 4x2
Solu.:
(i) f : R → R
f(x) = 2x + 1
f(1) = 2(1) + 1 = 3
f(2) = 2(2) + 1 = 5
f(-1) = 2(-1) + 1 = -1
f(0) = 2(0) + 1 = 1
It is a bijective function. Distinct elements of A have distinct images in B and every element in B has a pre-image in A.
(ii) f: R → R; f(x) = 3 – 4x2
f(1) = 3 – 4(12) = 3 – 4 = -1
f(2) = 3 – 4(22) = 3 – 16 = -13
f(-1) = 3 – 4(-1)2 = 3 – 4 = -1
It is not a bijective function since it is not one-one
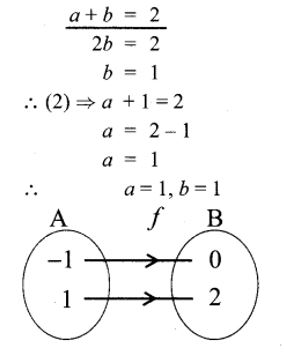
8. Let A = {-1, 1} and B = {0, 2}. If the function f: A → B defined by f(x) = ax + b is an onto function? Find a and b.
Solu.:
A= {-1, 1},B = {0, 2}
f: A → B, f(x) = ax + b
f(-1) = a(-1) + b = -a + b
f(1) = a(1) + b = a + b
Since f(x) is onto, f(-1) = 0
⇒ -a + b = 0 …(1)
& f(1) = 2
⇒ a + b = 2 …(2)
-a + b = 0
9. If the function f is defined by
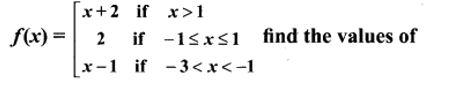
(i) f(3)
(ii) f(0)
(iii) f(-1.5)
(iv) f(2) + f(-2)
Solu.:
(i) f(3) ⇒ f(x) = x + 2 ⇒ 3 + 2 = 5
(ii) f(0) ⇒ 2
(iii) f (- 1.5) = x – 1
= -1.5 – 1 = -2.5
(iv) f(2) + f(-2)
f(2) = 2 + 2 = 4 [∵ f(x) = x + 2]
f(-2) = -2 – 1 = -3 [∵ f(x) = x – 1]
f(2) + f(-2) = 4 – 3 = 1
10. A function f: [-5,9] → R is defined as follows:
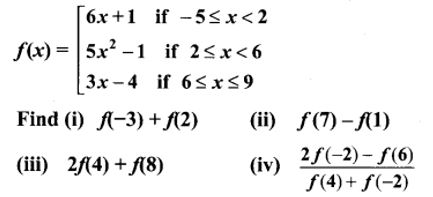
Solu.:
f : [-5, 9] → R
(i) f(-3) + f(2)
f(-3) = 6x + 1 = 6(-3) + 1 = -17
f(2) = 5 × 2 – 1 = 5(22) – 1 = 19
∴ f(-3) + f(2) = -17 + 19 = 2
(ii) f(7) – f(1)
f(7) = 3x – 4 = 3(7) – 4 = 17
f(1) = 6x + 1 = 6(1) + 1 = 7
f(7) – f(1) = 17 – 7 = 10
(iii) 2f(4) + f(8)
f(4) = 5x2 – 1 = 5 × 42 – 1 = 79
f(8) = 3x – 4 = 3 × 8 – 4 = 20
∴ 2f(4) + f(8) = 2 × 79 + 20 = 178
- The distance S an object travels under the influence of gravity in time t seconds is 1 2 given by S(t) = 13gt2+ at + b, where, (g is the acceleration due to gravity), a, b are constants. Check if the function S(t) is one-one.
Solu.:
S(t) = 12gt2+ at + b
Let the time be 1, 2, 3 …. n seconds
S(1) = 12g(1)2 + a(1) + b
= g2 + a + b
S(2) = 12 g(2)2 + a(2) + b
= 4g2 + 2a + b
= 2g + 2a + b
S(3) = 12 g(3)2 + a(3) + 6
= 92 g + 3a + b
For every different value of t, there will be different distances.
∴ It is a one-one function.
12. The function ‘t’ which maps temperature in Celsius (C) into temperature in Fahrenheit (F) is defined by t(C)= F where F = 95 C + 32. Find,
(i) t(0)
(ii) t(28)
(iii) t(-10)
(iv) the value of C when t(C) = 212
(v) the temperature when the Celsius value is equal to the Fahrenheit value.
Solu.:
Other Important Links for 10th Maths Book Back Answers Solutions:
For 10th Maths Book Chapter 1 book back question and answers, check the link – Samacheer Kalvi 10th Maths Chapter 1 Relation and Functions
Click here for the complete Samacheer Kalvi 10th Book Back Solution Guide PDF – Samacheer Kalvi 10th Maths Book Back Answers