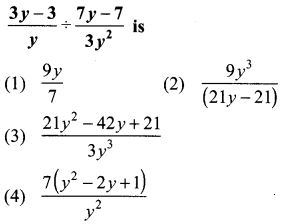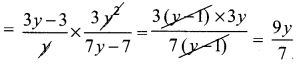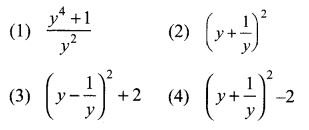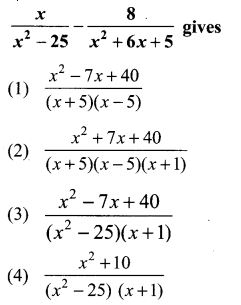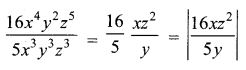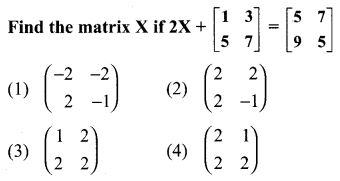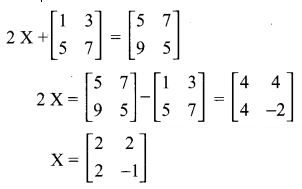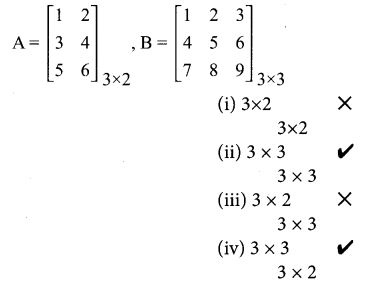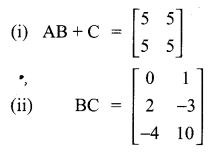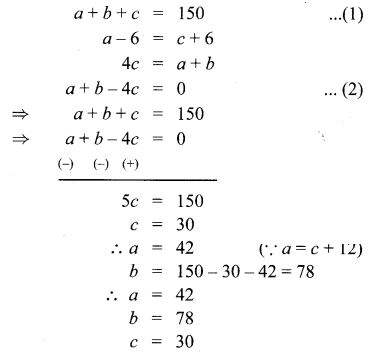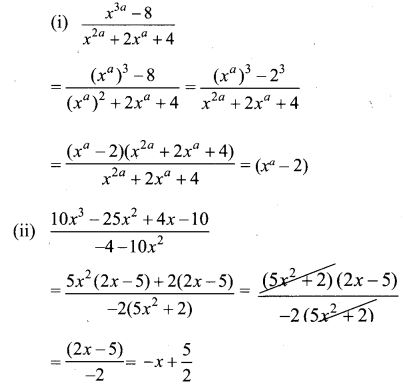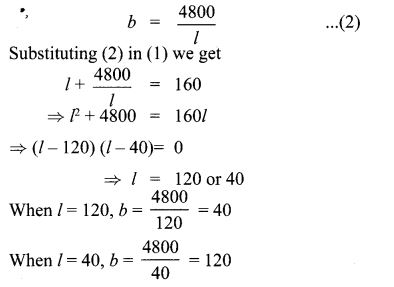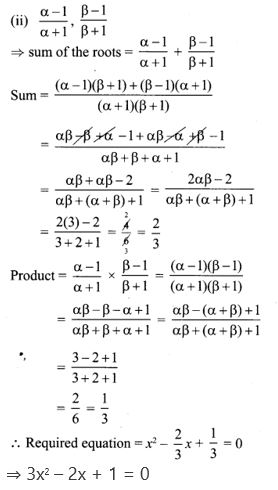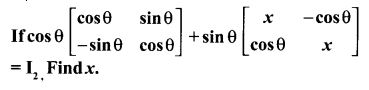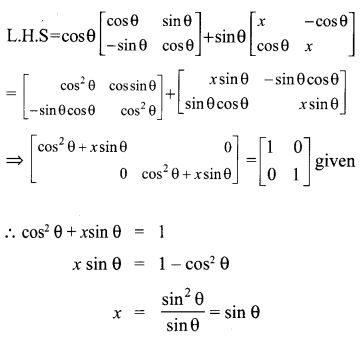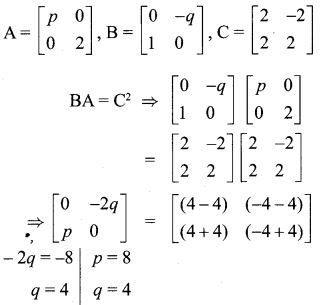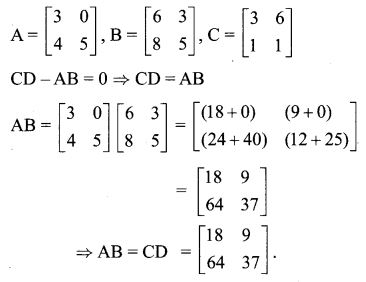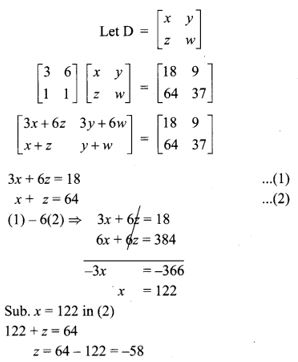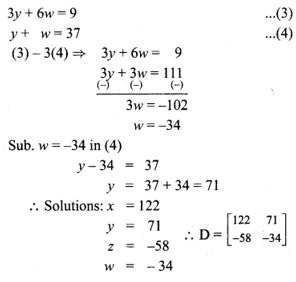10th Maths Book Back Question and Answers – Chapter 3 Exercise 3.19:
Samacheer Kalvi 10th Standard Maths Book Back Questions with Answers PDF uploaded and the same given below. Class-tenth candidates and those preparing for TNPSC exams can check the Maths Book Back Answers PDF below. Samacheer Kalvi Class 10th Std Maths Book Back Answers Chapter 3 Exercise 3.19 Solutions are available below. Check the complete Samacheer Kalvi 10th Maths – Algebra Ex 3.19 Book Back Answers below:
We also provide class 10th other units Maths Book Back One, Two, and Five Mark Solutions Guide on our site. Students looking for the 10th standard Maths Ex 3.19 – Algebra Book Back Questions with Answer PDF
For the complete Samacheer Kalvi 10th Maths Book Back Solutions Guide PDF, check the link – Samacheer Kalvi 10th Maths Book Back Answers
Samacheer Kalvi 10th Maths Book Back Answers – Ex 3.19 Algebra
Samacheer Kalvi 10th Maths Book Subject One Mark, Two Mark, Five Mark Guide questions and answers are below. Check Maths Book Back Questions with Answers. Take the printout and use it for exam purposes.
For Samacheer Kalvi 10th Maths Book PDF, check the link – 10th Maths Book PDF
Chapter 3
Exercise 3.19 Algebra
Multiple choice questions.
1. A system of three linear equations in three variables is inconsistent if their planes
(1) intersect only at a point
(2) intersect in a line
(3) coincides with each other
(4) do not intersect.
Solution:
(4) do not intersect
2. The solution of the system x + y – 3z = – 6, -7y + 7z = 7, 3z = 9 is …………
(1) x = 1, y = 2, z = 3
(2) x = -1, y = 2, z = 3
(3) x = -1, y = -2, z = 3
(4) x = 1, y = 2, z = 3
Answer:
(1) x = 1, y = 2, z = 3
Hint.
x + y – 3x = – 6 ….(1)
– 7y + 7z = 7 ….(2)
3z = 9 ….(3)
From (3) we get
z = 93 = 3
Substitute the value of z in (2)
-7y + 7(3) = 7
-7y = -14
Substitute the value of y = 2 and z = 3 in (1)
x + 2 – 3(3) = -6
x + 2 – 9 = -6
x = -6 + 7
x = 1
The value of x = 1, y = 2 and z = 3
3. If (x – 6) is the HCF of x2 – 2x – 24 and x2 – kx – 6 then the value of k is
(1) 3
(2) 5
(3) 6
(4) 8
Solution:
(2) 5
4.
Solution:
(1) 9y7
Solution:
(2) (y+1y)2
Hint:
y2+1y2≠[y+1/y]2
6.
Solution:
(3) x2−7x+40 / (x+5)(x−5)(x+1)
Hint:

7.
Solution:
8. Which of the following should be added to make x4 + 64 a perfect square ……….
(1) 4x2
(2) 16x2
(3) 8x2
(4) -8x2
Answer:
(2) 16x2
Hint.
x2 + 64 = (x2)2 + 82 – 2 × x2 × 8
= (x2 – 8)2
2 × x2 × 8 must be added
i.e, 16x2 must be added
9. The solution of (2x – 1)2 = 9 is equal to
(1) -1
(2) 2
(3) -1, 2
(4) None of these
Solution:
(3) -1, 2
Hint:
(2x – 1)2 = (±3)2
⇒ 2x – 1 = +3
2x – 1 = 3, 2x – 1 = – 3
2x = 4, 2x = – 2
x = 2,-1
10.The values of a and b if 4x4 – 24x3 + 76x2 + ax + b is a perfect square are
(1) 100, 120
(2) 10, 12
(3) -120, 100
(4) 12, 10
Solution:
(3) -120, 100
Hint:
11. If the roots of the equation q2x2 + p2x + r2 = 0 are the squares of the roots of the equation qx2 +px + r = 0, then q,p, r are in ______.
(1) A.P
(2) G.P
(3) Both A.P and G.P
(4) none of these
Solution:
(2) G.P
Hint: q2x2 + p2x + r2 = 0
(2) G.P.
12. Graph of a linear polynomial is a …………..
(1) straight line
(2) circle
(3) parabola
(4) hyperbola
Answer:
(1) straight line
13. The number of points of intersection of the T quadratic polynomial x2 + 4x + 4 with the X axis.
(1) 0
(2) 1
(3) 0 or 1
(4) 2
Solution:
(2) 1
(x + 2)2 = (x + 2)(x + 2)
= x = -2, -2 = 1
14.For the given matrix A = ⎡⎣⎢129341156137815⎤⎦⎥ the order of the matrix AT is
(1) 2 × 3
(2) 3 × 2
(3) 3 × 4
(4) 4 × 3
Solution:
(3) 3 × 4
Hint:
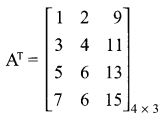
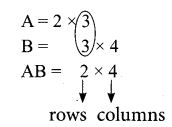
15. If A is a 2 × 3 matrix and B is a 3 × 4 matrix, how many columns does AB have
(1) 3
(2) 4
(3) 2
(4) 5
Solution:
(2) 4
Hint:
16. If a number of columns and rows are not equal in a matrix then it is said to be a …………..
(1) diagonal matrix
(2) rectangular matrix
(3) square matrix
(4) identity matrix
Answer:
(2) rectangular matrix
17. Transpose of a column matrix is
(1) unit matrix
(2) diagonal matrix
(3) column matrix
(4) row matrix
Solution:
(4) row matrix
18.
Solution:
(2) 2 2
19. Which of the following can be calculated from the given matrices
A = ⎡⎣⎢135246⎤⎦⎥, B = ⎡⎣⎢147258369⎤⎦⎥
(i) A2
(ii) B2
(iii) AB
(iv) BA
(1) (i) and (ii) only
(2) (ii) and (iiii) only
(3) (ii) and (iv) only
(4) all of these
Solution:
(3) (ii) and (iv) only
Hint:
20.
Solution:
(1) (i) and (ii) only
(2) (ii) and (iii) only
(3) (ii) and (iv) only
(4) all of these
Solution:
(1) (i) and (ii) only
Hint:
Exercise 3
3z = 3 ⇒ z = 1
(3) becomes, 3x + 2 = 20 ⇒ 3x = 20 – 2 = 18
x = 183 = 6
(1) becomes, 6 – 2y + 3(1) = 5 ⇒ 9 – 2y = 5
⇒ 9 – 5 = 2y ⇒ 2y = 4
∴ y = 42 = 2
∴ Solution set is {6, 2, 1}
2. One hundred and fifty students are admitted to a school. They are distributed over three sections A, B and C. If 6 students are shifted from section A to section C, the sections will have equal number of students. If 4 times of students of section C exceeds the number of students of section A by the number of students in section B, find the number of students in the three sections.
Solution:
Let the students in section A, B, C be a, b, c, respectively.
3. In a three-digit number, when the tens and the hundreds digit are interchanged the new number is 54 more than three times the original number. If 198 is added to the number, the digits are reversed. The tens digit exceeds the hundreds digit by twice as that of the tens digit exceeds the unit digit. Find the original number.
Solution:
Let the three digits numbers be 100a +10b + c.
100b + 10a + c = 3(100a + 10b + c) + 54 ………. (1)
100a + 106 + c + 198 = 100c + 106 + a ……… (2)
(b – a) = 2(b – c) ……… (3)
(1) ⇒ 100b + 10a + c = 300a + 30b + 3c + 54
⇒ 290a – 70b + 2c = -54
(2) ⇒ 99a – 99c = -198 ⇒ a – c = -2
⇒ a = c – 2
(3) ⇒ a + b – 2c = 0 ⇒ a + b = 2c
⇒ b = 2c – c + 2
⇒ b = c + 2
Substituting a, b in (1)
290(c – 2) – 70 (c + 2) + 2c = -54
290c – 580 – 70c – 140 + 2c = -54
222c = 666 ⇒ c = 3
a = 1, 6 = 5
∴ The number is 153.
4. Find the least common multiple of
xy (k2 + 1) + k(x2 + y2) and
xy(k2 – 1) + k (x2 – y2)
Answer:
xy (k2 + 1) + k(x2 + y2) = k2xy + xy + kx2 + ky2
= (k2xy + kx2) + (ky2 + xy)
= kx(ky + x) + y (ky + x)
= (ky + x) (kx + y)
xy (k2 – 1) + k(x2 – y2) = k2xy – xy + kx2 – ky2
= (k2xy + kx2) – xy – ky2
= kx(ky + x) -y (ky + x)
= (ky + x) (kx – y)
L.C.M. = (ky + x) (kx + y) (kx – y)
= (ky + x)(k2x2 – y2)
The least common multiple is
(ky + x) (k2x2 – y2)
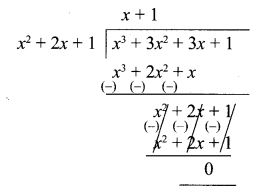
5.Find the GCD of the following by division algorithm 2x4 + 13.x3 + 21 x2 + 23x + 7, x3 + 3x2 + 3x + 1, x2 + 2x + 1.
Solution:
2x4 + 13x3 + 27x2 + 23x + 7,
x3 + 3x2 + 3x + 1, x2 + 2x + 1.
By division algorithm, first divide
∴ (x + 1)2 is G.C.D of x3 + 3x2 + 3x + 1 and x2 + 2x + 1.
Next let us divide
2x4 + 13x3 + 27x2 + 23x + 7 by x2 + 2x + 1
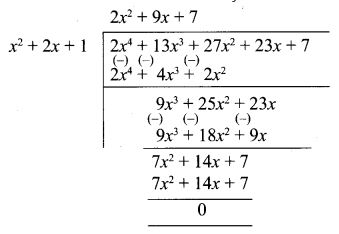
∴ G.C.D of 2x4 + 13x3 + 21 x2 + 23x + 7, x3 + 3x2 + 3x + 1, x2 + 2x + 1 is (x + 1)2.
6. Reduce the given Rational expressions to its lowest form
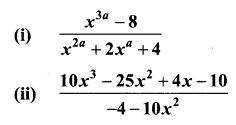
7.
8. Arul, Ravi and Ram working together can clean a store in 6 hours. Working alone, Ravi takes twice as long to clean the store as Arul does. Ram needs three times as long as Arul does. How long would it take each if they are working alone?
Solution:
Let Aral’s speed of working be x
Let Ravi’s speed of working be y
Let Ram’s speed of working be z
given that they are working together. ,
Let V be the quantum of work, x + y + z = w6 …………. (1)
Also given that Ravi takes twice the time as Aral for finishing the work.
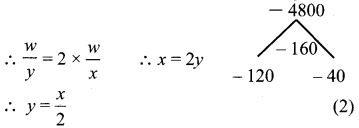
Also Ram takes 3 times the time as Aral for finishing the work.
∴ wz = 3 × wx
∴ x = 3z ∴ z = x3
Substitute (2) and (3) in (1),

9. Find the square root of 289x4 – 612x3 + 970x2 – 684x + 361
Solution:

10. Solve y+1−−−−√+2y−5−−−−−√ = 3.
Solution:
Squaring both sides
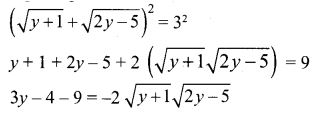
9y2 – 78y + 169 = 4 (y + 1)(2y – 5)
9y2 – 78y + 169 = 4 (2y2 + 2y – 5y – 5)
9y2 – 78y + 169 = 8y2 + 8y – 20y – 20
9y2 – 78y + 169 – 8y2 + 12y + 20 = 0
y2 – 66y + 189 = 0
y2 – 63y – 3y + 189 = 0
y(y – 63) – 3(y – 63) = 0
(y – 63)(y – 3) = 0
y = 63, 3
11. A boat takes 1.6 hours longer to go 36 kms up a river than down the river. If the speed of the water current is 4 km per hr, what is the speed of the boat in still water?
Solution:
Let the speed of boat in still water be ‘v’
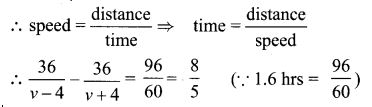
⇒ 36(v + 4) – 36(v – 4) = 85 (v – 4) (v + 4)
⇒ 36v + 144 – 36v + 144 = 85 (v2 – 4v + 4v – 16)
⇒ 288 = 85 v2 – 1285 ⇒ 8v2 – 128 = 1440
⇒ 8v2 = 1568 ⇒ v2 = 196 v = ±14
∴ Speed of the boat = 14 km/hr. (∵ speed cannot be -ve)
12. Is it possible to design a rectangular park of perimeter 320 m and area 4800 m2? If so find its length and breadth.
Solution:
Let the length and breadth of the rectangle be lm and bm
Given 2(1 + b)
⇒ l + b = 160 ………. (1)
Also l b = 4800
∴ Length and breadth of the rectangular park is 120m and 40 m
13. At t minutes past 2 pm, the time needed to 3 pm is 3 minutes less than t24 Find t.
Solution:
60 – t = t24 – 3
⇒ t2 – 12 = 240 – 4t
⇒ t2 + 4t – 252 = 0
⇒ t2 + 18t – 14t – 252 = 0
⇒ t(t + 18) – 14(t + 18) = 0
⇒ (t + 18) (t – 14) = 0
∴ t = 14 or t = -18 is not possible.
14. The number of seats in a row is equal to the total number of rows in a hall. The total number of seats in the hall will increase by 375 if the number of rows is doubled and the number of seats in each row is reduced by 5. Find the number of rows in the hall at the beginning.
Solution:
Let the no of seats in each row be x

⇒ 2x2 – 10x = x2 + 375
⇒ x2 – 10x – 375 = 0
⇒ x2 – 25x + 15x – 375 = 0
⇒ x (x – 25) + 15 (x – 25) = 0
⇒ (x – 25) (x + 15) = 0
⇒ x = 25, x = -15, x > 0
∴ 25 rows are in the hall.
15.If a and b are the roots of the polynomial f(x) = x2 – 2x + 3, find the polynomial whose roots are
(i) α + 2, β + 2
(ii) α−1α+1,β−1β+1
Solution:
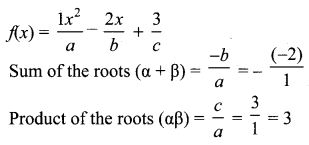
(i) α + 2, β + 2 are the roots (given)
Sum of the roots = α + 2 + β + 2
= α + β + 4
= 2 + 4 = 6
Product of the roots = (α + 2) (β + 2)
= αβ + 2α + 2β + 4
= αβ + 2(α + β) + 4
= 3 + 2 × 2 + 4
= 3 + 4 + 4 = 11
∴ The required equation = x2 – 6x + 11 = 0.
16. If -4 is a root of the equation
x2 + px – 4 = 0 and if the equation
x2 + px + q = 0 has equal roots, find the values of p and q.
Answer:
Let p(x) = x2 + px – 4
– 4 is the root of the equation
P(-4) = 0
16 – 4p – 4 = 0
-4p + 12 = 0
-4p = -12
p = 124 = 3
The equation x2 + px + q = 0 has equal roots
x2 + 3 x + q = 0
Here a = 1, b = 3, c = q
since the roots are real and equal
b2 – 4 ac = 0
32 – 4(1)(q) = 0
9 – 4q = 0
9 = 4q
q = 94
The value of p = 3 and q = 94
17.Two farmers Senthil and Ravi cultivates three varieties of grains namely rice, wheat and ragi. If the sale (in ₹) of three varieties of grains by both the farmers in the month of April is given by the matrix.

May month sale (in ₹) is exactly twice as that of the April month sale for each variety.
(i) What is the average sales of the months April and May.
(ii) If the sales continues to increase in the same way in the successive months, what will be sales in the month of August?
Solution:
18.
Solution:
19.
Solution:
20.
Other Important Links for 10th Maths Book Back Answers Solutions:
For 10th Maths Chapter 3 book back question and answers, check the link – Samacheer kalvi 10th Maths Chapter 3 Algebra
Click here for the complete Samacheer Kalvi 10th Maths Book Back Solution Guide PDF – 10th Maths Book Back Answers