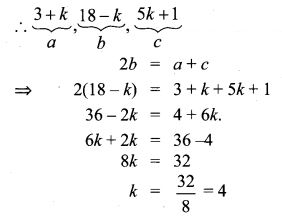10th Maths Book Back Question and Answers – Chapter 2 Exercise 2.5:

Samacheer Kalvi 10th Standard Maths Book Back Questions with Answers PDF uploaded and the same given below. Class-tenth candidates and those preparing for TNPSC exams can check the Maths Book Back Answers PDF below. Samacheer Kalvi Class 10th Std Maths Book Back Answers Chapter 2 Exercise 2.5 Solutions are available below. Check the complete Samacheer Kalvi 10th Maths – Numbers and Sequences Ex 2.5 Book Back Answers below:

We also provide class 10th other units Maths Book Back One and Two Mark Solutions Guide on our site. Students looking for the 10th standard Maths Ex 2.5 – Numbers and Sequences Book Back Questions with Answer PDF

For the complete Samacheer Kalvi 10th Maths Book Back Solutions Guide PDF, check the link – Samacheer Kalvi 10th Maths Book Back Answers

Samacheer Kalvi 10th Maths Book Back Answers – Ex 2.5 Numbers and Sequences

Samacheer Kalvi 10th Maths Book Subject One Mark, Two Mark, Five Mark Guide questions and answers are below. Check Maths Book Back Questions with Answers. Take the printout and use it for exam purposes.

For Samacheer Kalvi 10th Maths Book PDF, check the link – 10th Maths Book PDF

Chapter 2

Ex 2.5 – Numbers and Sequences

1. Check whether the following sequences are in A.P.
(i) a – 3, a – 5, a – 7, ………
(ii) 12,13,14,14, ………..
(iii) 9, 13, 17, 21, 25, ………
(iv) −13,0,13,23,………..
(v) 1,-1, 1,-1, 1,-1,…
Solution:
To prove it is an A.P, we have to show d = t₂ – t₁ = t₃ – t₂.
(i) a – 3, a – 5, a – 7………
t₁,t₂,t₃
d = t₂ – t₁ = a – 5 – (a – 3) = a – 5 – a + 3 = -2
∴ d = -2    ∴ It is an A.P.
d = t₃ – t₂ = a – 7 – (a – 5) = a – 7 – a + 5 = -2

(v) 1,-1, 1,-1, 1,-1,…
d = t₂ – t₁ = -1 -1 = -2
d = t₃ – t₂ = 1 – (-1) = 2
-2 ≠ 2 ∴ It is not an A.P.

2. First term a and common difference d are given below. Find the corresponding A.P.
(i) a = 5, d = 6
(ii) a = 7, d = 5
(iii) a = 34, d = 12
Solution:
(i) a = 5, d = 6
A.P a, a + d, a + 2d, ………
= 5, 5 + 6, 5 + 2 × 6, ………
= 5, 11, 17,…
(ii) a = 7,d = -5
A.P. = a,a + d,a + 2d,…
= 7,7 + (-5), 7 + 2(-5), ……….
= 7, 2, -3, …….,…
(iii) a = 34, d = 12

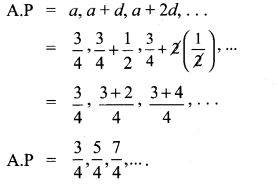
3. Find the first term and common difference of the Arithmetic Progressions whose nth terms are given below

(i) t_n = -3 + 2n
Answer:
t_n = -3 + 2 n
t₁ = -3 + 2(1) = -3 + 2
= -1
t₂ = -3 + 2(2) = -3 + 4
= 1
First term (a) = -1 and
Common difference
(d) = 1 – (-1) = 1 + 1 = 2

(ii) t_n = 4 – 7n
Answer:
t_n = 4 – 7n
t₁ = 4 – 7(1)
= 4 – 7 = -3
t₂ = 4 – 7(2)
= 4 – 14 = -10
First term (a) = – 3 and
Common difference (d) = 10 – (-3)
= – 10 + 3
= – 7

4. Find the 19th term of an A.P. -11, -15, -19, ………..
Solution:
A.P = -11, -15, -19, ……..
a = -11
d = t₂ – t₁ =-15-(-11)
= -15 + 11
= -4
n = 19
∴ t_n = a + (n – 1)d
t₁₉ = -11 + (19 – 1)(-4)
= -11 + 18 × -4
= -11 – 72
= -83

5. Which term of an A.P. 16, 11, 6, 1,… is -54?
Answer:
First term (a) = 16
Common difference (d) = 11 – 16 = -5
t_n = – 54
a + (n – 1) d = -54
16 + (n – 1) (-5) = -54
54 + 21 = -54
54 + 21 = 5n
75 = 5n
n = 755 = 15
The 15^th term is – 54

6. Find the middle term(s) of an A.P. 9, 15, 21, 27, ……. ,183.
Solution:
A.P = 9, 15, 21, 27,…, 183
No. of terms in an A.P. is
n = l−ad + 1
a = 9, l = 183, d = 15 – 9 = 6
∴ n = 183−96 + 1
= 1746 + 1
= 29 + 1 = 30
∴ No. of terms = 30. The middle must be 15th term and 16th term.
∴ t₁₅ = a + (n – 1)d
= 9 + 14 × 6
=9 + 84
= 93
t₁₆ = a + 15 d
= 9 + 15 × 6
= 9 + 90 = 99
∴ The middle terms are 93, 99.

7. If nine times the ninth term is equal to the fifteen times a fifteenth term, Show that six times twenty-fourth term is zero.
Answer:
t_n = a + (n – 1)d
9 times 9^th term = 15 times 15^th term
9t₉ = 15 t₁₅
9[a + 8d] = 15[a + 14d]
9a + 72d = 15a + 210d
9a – 15a + 72 d – 210 d = 0
-6a – 138 d = 0
6a + 138 d = 0
6 [a + 23 d] = 0
6 [a + (24 – 1)d] = 0
6 t₂₄ = 0
∴ Six times 24th terms is 0.

8.If 3 + k, 18 – k, 5k + 1 are in A.P. then find k.
Solution:
3 + k, 18 – k, 5k + 1 are in A.P
⇒ 2b = a + c if a, b, c are in A.P

9. Find x,y and z gave that the numbers x,
10, y, 24, z are in A.P.
Answer:
x, 10, y, 24, z are in A.P
t₂ – t₁ = 10 – x
d = 10 – x …..(1)
t₃ – t₂ = y – 10
d = y – 10 ……(2)
t₄ – t₃ = 24 – y
d = 24 – y …..(3)
t₅ – t₄ = z – 24
d = z – 24 …..(4)
From (2) and (3) we get
y – 10 = 24 – y
2y = 24 + 10
2y = 34
y = 17
From (1) and (2) we get
10 – x = y – 10
– x – y = -10 -10
-x -y = -20
x + y = 20
x + 17 = 20(y = 17)
x = 20 – 17 = 3
From (1) and (4) we get
z – 24 = 10 – x
z – 24 = 10 – 3 (x = 3)
z – 24 = 7
z = 7 + 24
z = 31
The value of x = 3, y = 17 and z = 31

10. In a theatre, there are 20 seats in the front row and 30 rows were allotted. Each successive row contains two additional seats than its front row. How many seats are there in the last row?
Solution:
t₁ = a = 20
t₂ = a + 2 = 22
t₃ = a + 2 + 2 = 24 ⇒ d = 2
∴ There are 30 rows.
t₃₀ = a + 29d
= 20 + 29 × 2
= 20 + 58
= 78
∴ There will be 78 seats in the last row.

11. The Sum of three consecutive terms that are in A.P. is 27 and their product is 288. Find the three terms.
Answer:
Let the three consecutive terms be a – d, a and a + d
By the given first condition
a – d + a + a + d = 27
3a = 27
a = 273 = 9
Again by the second condition
(a – d) (a) (a + d) = 288
a (a² – d²) = 288
9(81 – d²) = 288 (a = 9)
81 – d² = 2889
81 – d² = 32
∴ d² = 81 – 32
= 49
d = 49−−√ = ± 7
When a = 9, d = 7
a + d = 9 + 7 = 16
a = 9
a – d = 9 – 7 = 2
When a = 9, d = -7
a + d = 9 – 7 = 2
a = 9
a – d = 9 – (-7) = 9 + 7 = 16
The three terms are 2, 9, 16 (or) 16, 9, 2

12. The ratio of 6th and 8^th term of an A.P is 7:9. Find the ratio of 9^th term to 13^th term.
Solution:
t6t8=79
a+5da+7d = 79
9a + 45d = 7a + 49d
9 a + 45 – 7d = 7a + 49 d
9a + 45d – 7a – 49d = 0
2a – 4d = 0 ⇒ 2a = 4d
a = 2d
Substitue a = 2d in

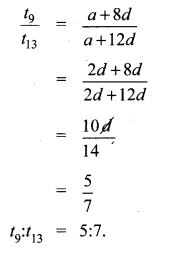
13. In a winter season let us take the temperature of Ooty from Monday to Friday to be in A.P. The sum of temperatures from Monday to Wednesday is 0° C and the sum of the temperatures from Wednesday to Friday is 18° C. Find the temperature on each of the five days.
Solution:
Let the five days temperature be (a – d), a, a + d, a + 2d, a + 3d.
The three days sum = a – d + a + a + d = 0
⇒ 3a = 0 ⇒ a = 0. (given)
a + d + a + 2d + a + 3d = 18
3a + 6d = 18
3(0) + 6 d = 18
6d = 18
d = 186 = 3
∴ The temperature of each five days is a – d, a, a + d, a + 2d, a + 3d
0 – 3, 0, 0 + 3, 0 + 2(3), 0 + 3(3) = -3°C, 0°C, 3°C, 6°C, 9°C

14. Priya earned ₹ 15,000 in the first month. Thereafter her salary increased by ₹1500 per year. Her expenses are ₹13,000 during the first year and the expenses increases by ₹900 per year. How long will it take for her to save ₹20,000 per month.
Solution:

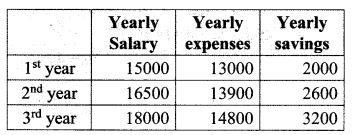
We find that the yearly savings is in A.P with a₁ = 2000 and d = 600.
We are required to find how many years are required to save 20,000 a year …………..
a_n = 20,000
a_n = a + (n – 1)d
20000 = 2000 + (n – 1)600
(n – 1)600 = 18000
n – 1 = 18000600 = 30
n = 31 years

Other Important Links for 10th Maths Book Back Answers Solutions:

For 10th Maths Book chapter 2 book back question and answers, check the link – Samacheer kalvi 10th Maths Chapter 2 Numbers and Sequences

Click here for the complete Samacheer Kalvi 10th Book Back Solution Guide PDF – 10th Maths Book Back Answers